
トラスって何?

三角形の骨組み構造です。
鉄橋に使われてますよ
- トラスの解き方がわかる
トラスとは
トラスとは、直線の部材を3本組み合わせて、三角形の骨組み構造を作ったものです。
3つの辺の長さが決まると形状が定まり形が変化しなくなります。このように部材の端っこをピンで結合して組み合わせた骨組み構造物をトラス構造物と言います。

3辺の長さが決まると三角形の形が決まります。
この性質を利用したものがトラスです。
トラスの特徴
- 部材の両端は接点になっている
- トラスには軸力のみ働く
- 外力は全て接点に作用する

大事なことは、トラスには軸力のみが働くということです。
トラスの部材力の解き方:基本的な考え方

部材力って?

部材力とは、部材のひとつひとつに働く力のことです。
トラスの部材力の求め方も、はりと同じです。
- 支点反力を求める
- 部材を仮想的に切断する
- 力のつり合いを求める

具体的に解いてみましょう!
トラスの部材力の解き方:例題

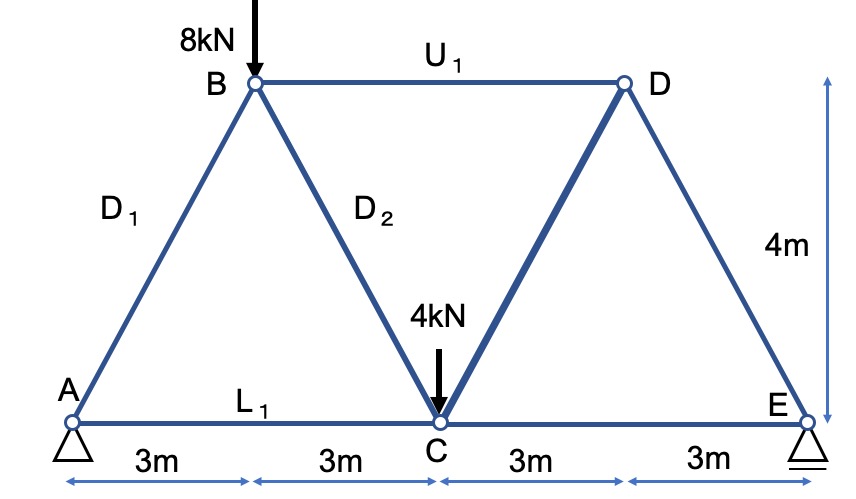
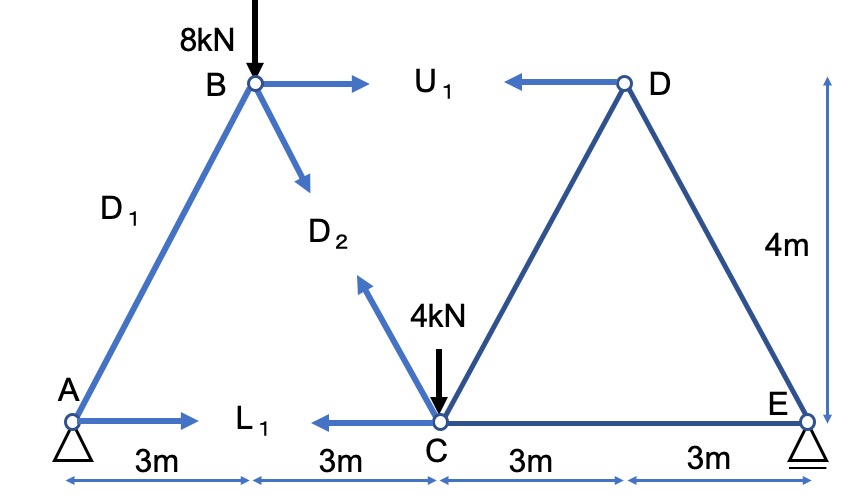
上の図のトラスの部材力を求めてみましょう。
上の図のU1、L1、D1、D2について求めてみましょう
トラスの部材力の解き方:接点法
接点法では、各接点ごとの力のつり合いから部材力を求めます。

まずは、支点反力を求めましょう。
支点反力を求める
支点反力の求め方はこちらも参考になります。

トラスの場合も同じです。次のように単純に考えてみましょう。
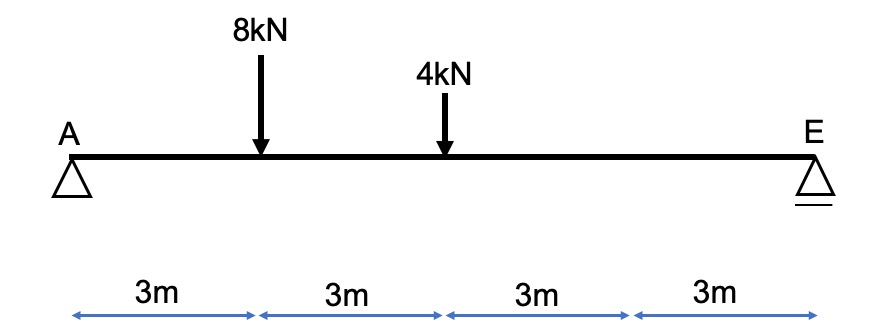
支点反力はこうなります。

点A周りの曲げモーメントから求めることができます。
VA=8kN
VE=4kN
点Aのつり合いからを求める
点Aの力のつり合いからD1とL1の部材力について求めてみましょう。
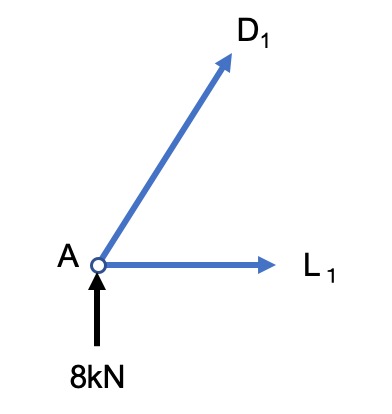

これだけで求められるの?

三角形の性質を利用しましょう。
底辺3m、高さ4mの三角形の斜辺は5mです。
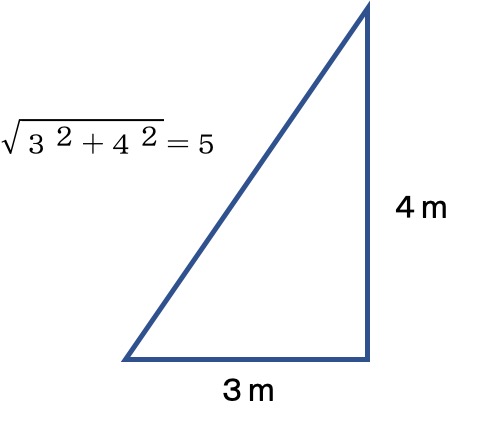
つまり、D1は次のように分けられます。
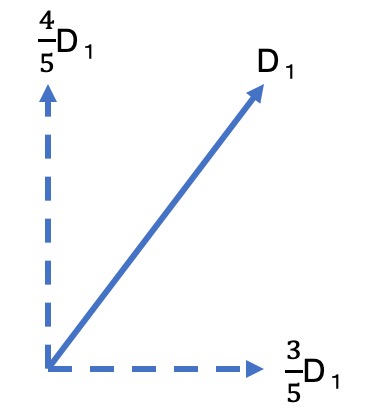

これを使って力のつり合い式を解いてみましょう。
鉛直方向
(4/5)D1+VA=0
D1=-10
水平方向
(3/5)D1+L1=0
L1=(3/5)×(-10)
L1=-6kN
点Bのつり合いから求める

さっきと同じように求めたらいいんですね!

そうです。次のように図を書きましょう。
D1は先ほど求めましたね。
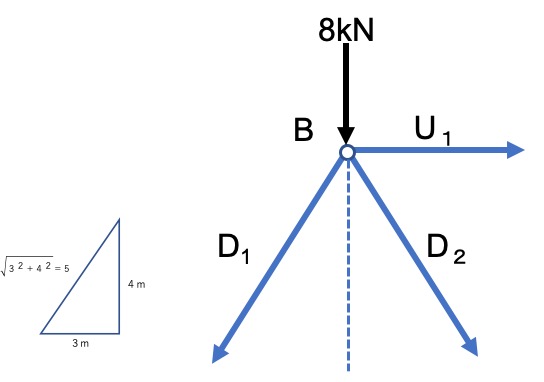
鉛直方向
(4/5)D1+(4/5)D2+8=0
(4/5)D2=-8-(4/5)×(-10)
D2=0
水平方向
(3/5)D1=U1+(3/5)D2
U1=(3/5)×(-10)-(3/5)×0
U1=-6

やることは力のつり合いを解くだけですね!
点Cからつり合いを求める
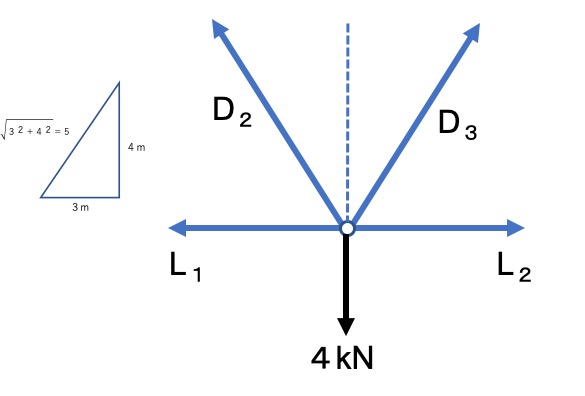

同じように求めていきましょう!
鉛直方向
(4/5)D2+(4/5)D3=4
(4/5)D3=4-(4/5)×0
D3=4*(5/4)
D3=5
水平方向
(3/5)D2+L1=(3/5)D3++L2
L2=-(3/5)D2+L1-(3/5)D3
L2=-(3/5)×0+6-(3/5)×5
L2=3

全て求められました!
ちなみに、全部の部材力を図に書くとこんな感じです。
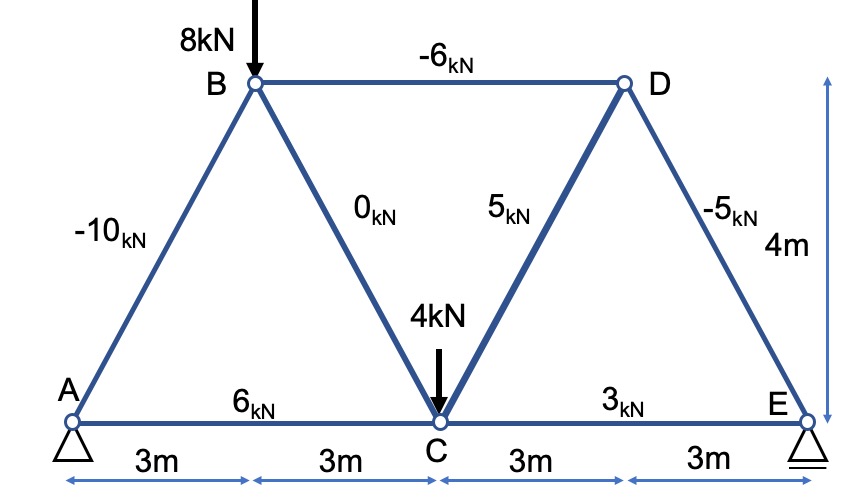

切断法は支点反力のある点から順番に解いていく方法ですね。
トラスの部材力の解き方:断面法

断面法って何?

任意の場所の部材力を直接求める方法です。
断面法は、トラスを任意の位置で切断し、断面のつり合いから部材力を求める方法です。

試しに、L1、U1、D2を求めてみましょう。
仮想的に次のように切断します。
支点反力を求める

さっき求めましたね。

左半分でつり合い式を書きましょう!
VA=8
VE=4
鉛直方向のつり合いを求める
VA=(4/5)D2+8
(4/5)D2=VA-8
D2=0
曲げモーメントのつり合いを求める

力がいっぱい働いている点B周りの曲げモーメントを求めてみましょう。
VA×3=L1×4
L1=(3/4)×VA
L1=6
水平方向のつり合いを求める
U1+L1+(3/5)D2=0
U1=-L1-(3/5)D2
U1=-6

断面法を使うと一気に求められますね!
トラスの部材力の求め方:まとめ
トラスの部材力を求める方法は次の2つです。
- 接点法
- 断面法

どちらの方法もやることは一緒です。
- 支点反力を求める
- 力のつり合いを求める

さらに問題を解いてトラスの部材力の求め方をマスターしましょう!
おすすめポイント
・問題を解くのに必要な解説だけが書いてある
・問題の解説が省略されていない
・構造力学だけじゃなく水理学・地盤工学も入っている
結論:コストパフォーマンス最強
三力の勉強はこれ一冊で十分です。
以上、とたん(@act_ik)でした。


