
断面力図の書き方がわかりません。
テストまで時間がないので簡単に書ける方法が知りたいです。
断面力図の書き方は簡単です。
断面力の求め方は『【断面力とは】断面力の求め方や応力との違いを解説』で解説していますので、こっちのページも開きつつ、読むとわかりやすいはず。
先にネタバレすると、断面力には一定のルールがあります。それが以下の図の通り
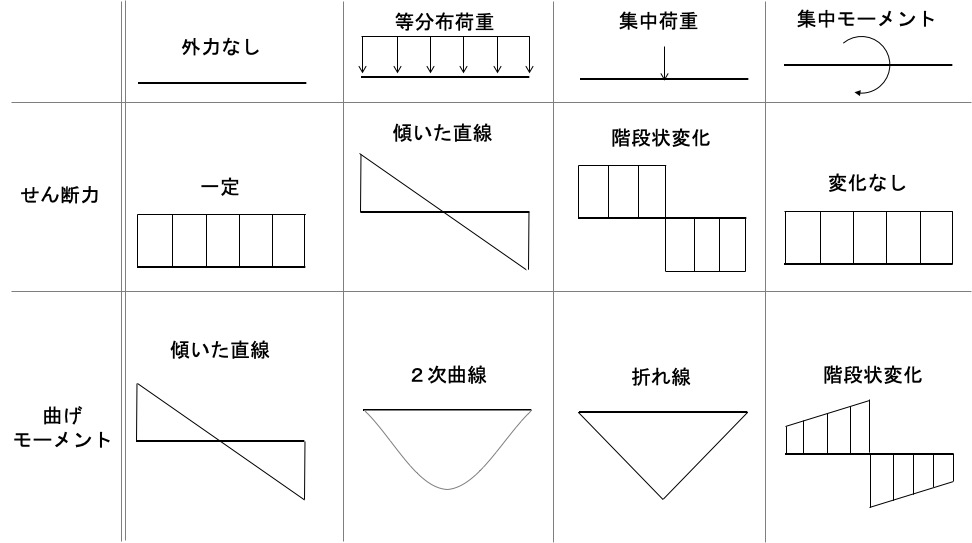
この図を覚えるととりあえず断面力図は書けます。
明石高専の都市システム工学科(土木)出身の僕が断面力図の書き方の基本と裏技を紹介します。
目次
単純ばりのせん断力図・曲げモーメント図の書き方

例題として、単純ばりに分布荷重がかかっている問題を解いてみましょう。
ちなみに、分布荷重については『分布荷重は集中荷重に置き換えよう【計算方法は面積を求めるだけ】』で解説しています。
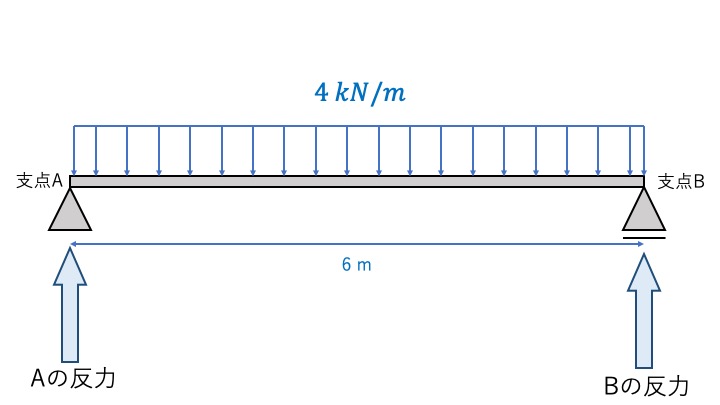
単純ばりの断面力の基本的な書き方は以下の通り。
ステップはいっぱいありますが、簡単です。
左側から計算した方がわかりやすいのですが、別に右側から計算してもOKです。
断面力図の書き方①外力から支点反力を求める
外力から支点反力を求めましょう。支点反力の求め方は『支点反力の求め方をわかりやすく解説します【縦と横に分解しましょう】』で解説しています。
支点反力の計算は以下の通り。
ですので、Aの反力もBの反力も\(12kN\)
なので、こうなります。
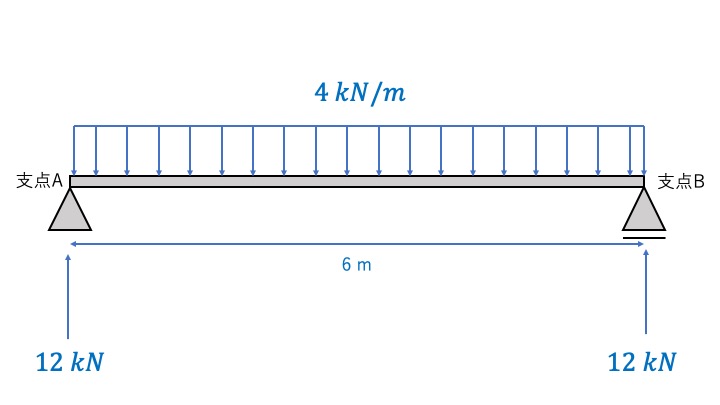
断面力図の書き方②外力のある点で分割する
外力のある点で分割します。分布荷重の場合は分布荷重の重心の点でOK。
この例題の場合は、単純ばりの中心で分割しましょう。
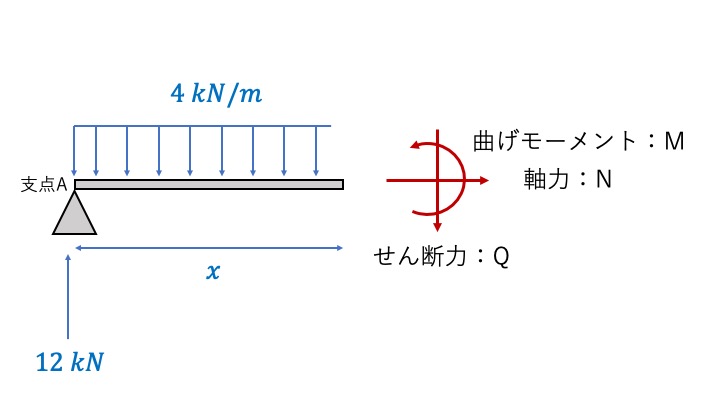
断面力図の書き方③左側から分割した点までの断面力を計算する
単純ばりの左側から分割した点まで、距離を\(x\)と置いて計算します。
大事なことは以下の2つ
支点Aから断面力を計算する
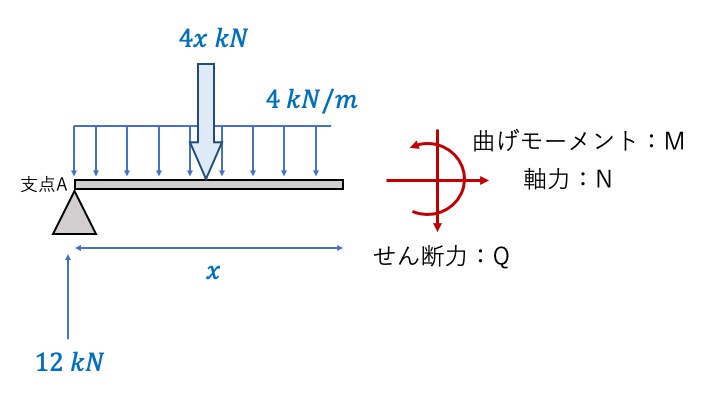
計算すると以下の通りになります。
断面力図の書き方④計算した断面力を図にする
計算した断面力から断面力図を書きます。
今回の例題では、左右対称なので、真ん中まで書いて対称にすればOKです。
せん断力図の書き方
せん断力図の式は\(Q=-4x+12\)なので、以下の通りに考えます。
せん断力Qは1次式なので直線で繋ぎます。
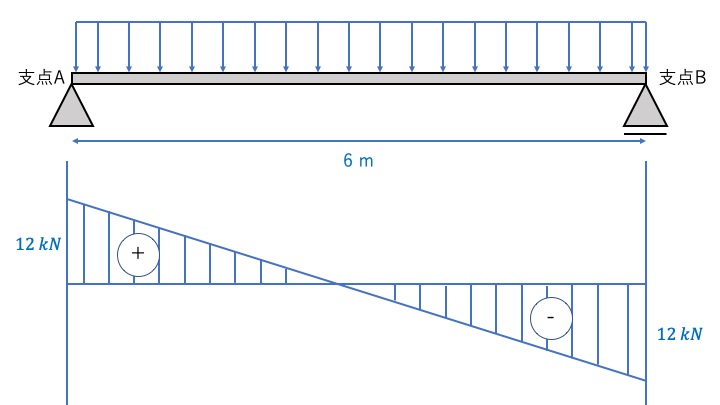
曲げモーメント図の書き方
曲げモーメントの式は\(M=12x-2x^{2}\)なので、以下の通りに考えます。
曲げモーメントMは2次式なので曲線で繋ぎます。
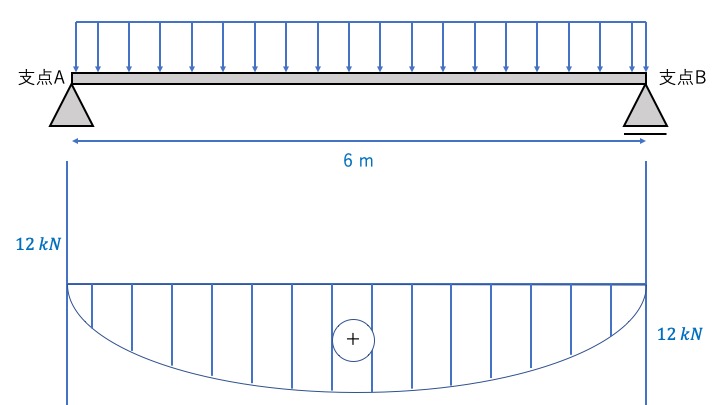
断面力図を外力から直接書いてみる
構造力学の断面力図を書くためには、荷重とそれに対応する断面力図を覚えるといい。
後は、その荷重のかかっている点の断面力のみ求めればOKです。
下の図について、一緒に解いてみましょう。
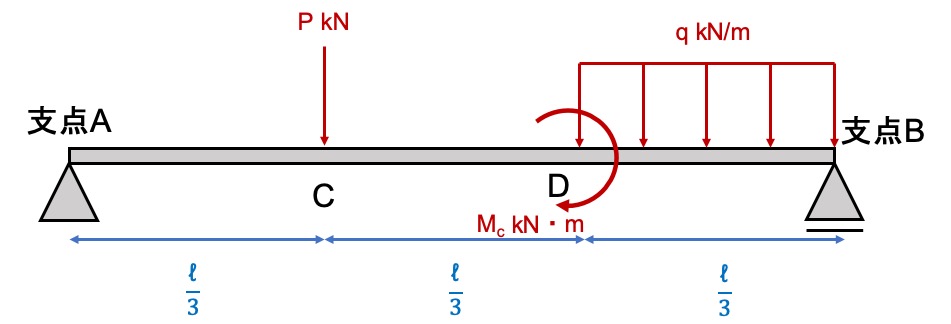
断面力図の書き方①せん断力図の特徴

せん断力図の特徴を見ていきましょう。
せん断力図には次の5つの特徴があります。
まずは、支点反力をVA、VBとして、上の5つの特徴から断面力図を書いてみましょう。

上の特徴から、①、②、③、⑤が該当します。
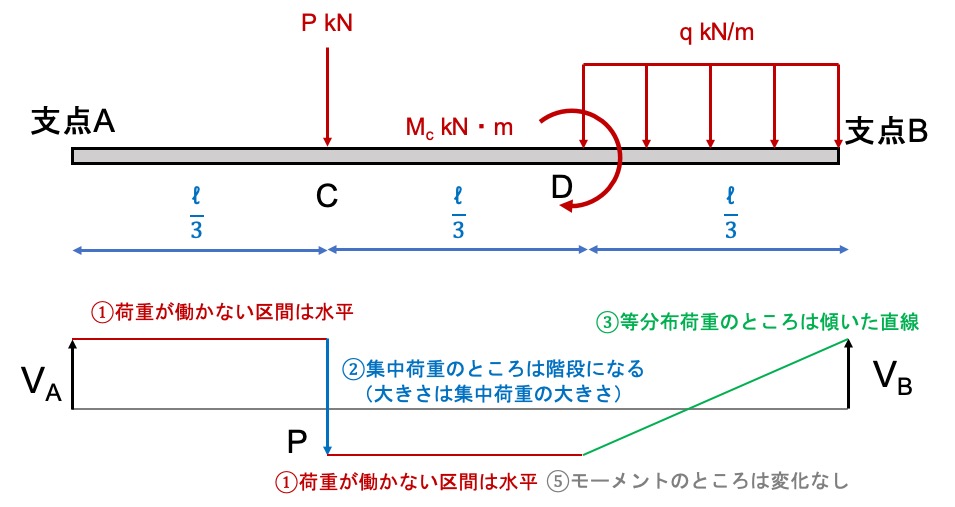
このように、図だけで書くことができます。

図のプラスとマイナスは支点反力から求めることができます。
支点反力についても詳しく知りたい人は『【簡単】支点反力の求め方』で解説していますので、合わせてご覧ください。
断面力図の書き方②曲げモーメント図の特徴
曲げモーメントの特徴は次のとおりです。
上の例題に当てはめると次のような断面力図になります。
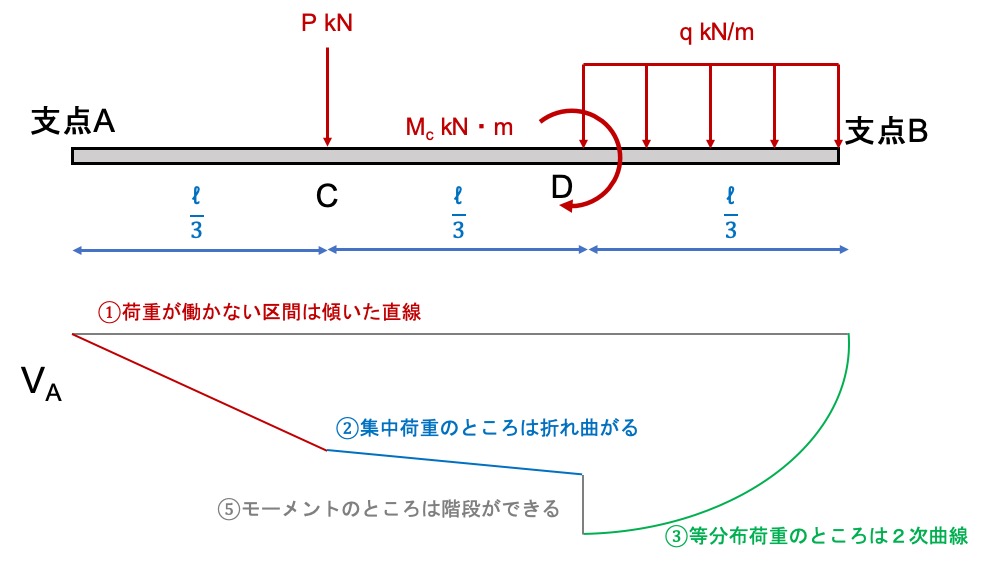

せん断力図と同じようにプラスとマイナスは支点反力を計算すると求めることができます。
断面力図の書き方は形で覚えてしまおう【裏技】
特徴をまとめてみてみましょう。

この表を覚えておくと、問題を解いた後の答え合わせにも使えます。
裏技を覚えた上で、断面力図の書き方を練習しよう
上記の裏技を覚えるために、1問でも多く問題集を解きましょう。
学校の教科書の問題もいいですが、僕は問題集を買って解くことをオススメしてます。
『構造力学はたくさん問題を解いた人の勝ち』です。
オススメの問題集は『構造力学が苦手な人が読むべきオススメ参考書5選』で解説しています。


