
断面力図の書き方がわかりません。具体的な書き方を教えてほしいです。
このままでは構造力学の単位を落としそうなので、できるだけわかりやすく解説をお願いします。
断面力図の書き方を解説します。
この記事を見ながら断面力図が書けるようになりましょう。
- 断面力図の書き方は簡単
- この記事を見た後にするべきことは問題をたくさん解くこと
この記事を書く僕は、明石高専の都市システム工学科(土木)出身。
構造力学の単位もちゃんと取ってます。
この記事をお気に入り登録しておくと見返すのが楽ですよ。
目次
断面力図の書き方は簡単

はりの断面力図を書いてみましょう。
はりの断面力図の書き方:基本的な考え方
断面力図は、はりの端っこから端っこまでの断面力を求めて、図にすることで書くことができます。

端から端まで・・・

力のある点だけ求めればOKです!
断面力図を求めるための必要なポイントは次の3つです。
- 支点反力を求める
- 端っこから力のある点ごとに区切る
- 断面力を求める
この3つの手順ではりの断面力図を書いてみましょう。
断面力図の書き方:はりの断面力図を解いてみる
はりの支点反力を求める
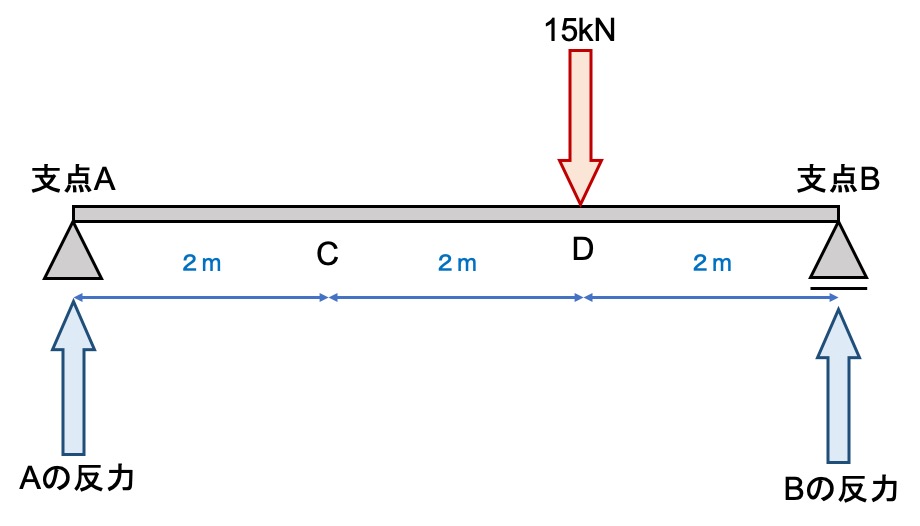
上の図のはりの支点反力を求めてましょう。
支点反力の求め方はこちらで解説しています。
水平方向
HA+HB=0

水平方向の力は働いてませんね。
鉛直方向
VA+VB=15kN
VA ×0m+VB×6m=15kN×4m

これを計算すると支点反力が求められます!
VA=5kN
VB=10kN
端っこから力のある点ごとに区切る
断面力図を書くためには、端っこから力のある点ごとに区切って考えます。

区切る・・・?
具体的には、力のある点から力のある点までの長さをX(変数)にして考えます。
つまり、長さに比例するモーメントは長くなるほど大きくなるということです。
断面力の分布を描く
長さをX(変数)にして断面力を求めると、あとはそれを図にするだけです。

ここまで来たら、あとは簡単です!
断面力図の書き方:実例

上の図を実例に求めてみましょう。
支点反力は求めましたね。
VA=5kN
VB=10kN
力のある点から力のある点の断面力を求めていきましょう。
上の図では、次の2つです。
- 支点AからD点
- D点から支点B
支点AからD点まで
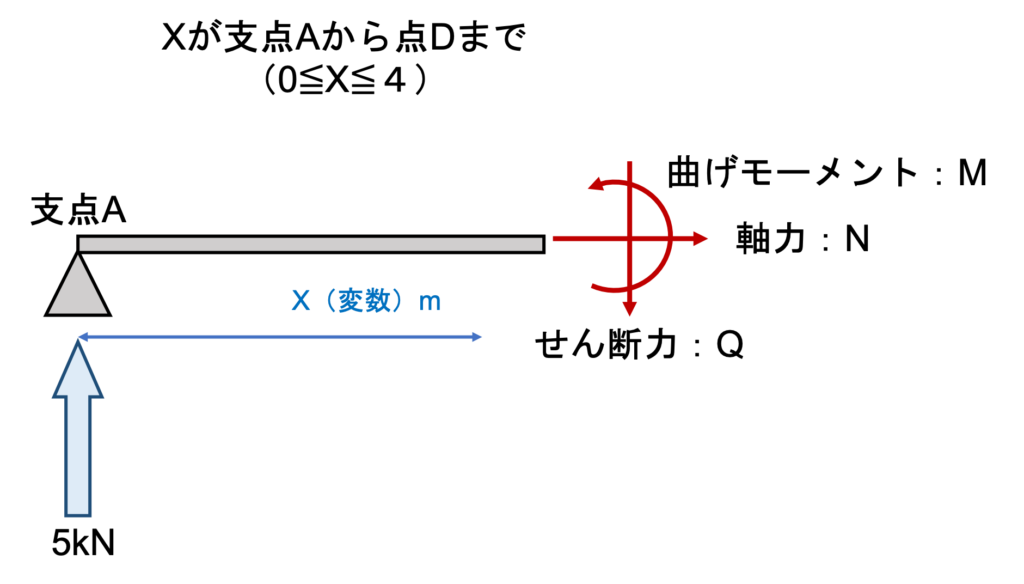

支点AからD点の断面力を求めてみましょう!
軸力
N=0kN

軸力は働いていませんね。
せん断力
VA=N
つまり、N=5kN

支点Aから点Dではどこでも、5kNの力が働いているということですね。
曲げモーメント

曲げモーメントだけ注意が必要です!
モーメントは長さに比例します!
曲げモーメントMにつり合う力を考えてみましょう。
M=VA × X
つまり、M=5kN× X

あれ?
Xが残ったままだけど?
曲げモーメントはX(変数)に従った大きさになります。
つまり、支点Aでは0で点Dでは、20kN・mになります。

確かに、支点Aでは曲がる力は働いてませんよね。
同じように、点Dから支点Bまでも求めてみましょう。
点Dから支点Bまで
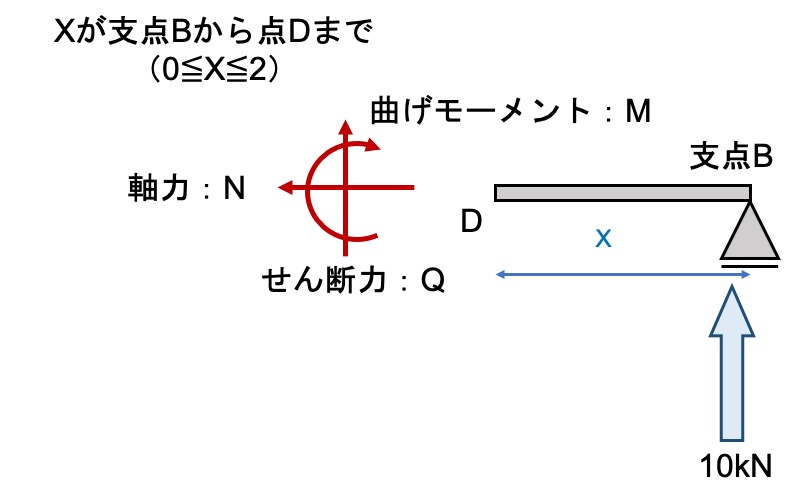

さっきと同じ感じでやればいいんですね!
軸力
N=0kN
せん断力
VB=-Q
つまり、Q=-10kN

図を見るとQと10kNが同じ向きになっています。
つまり、Qは下向きの力です。
曲げモーメント
M=VB × X
つまり、M=10kN× X

これで、全ての断面力を求めることができました!
ちなみに、点Dの曲げモーメントの大きさはどちらで計算しても同じ値になります。

それでは、図を書いてみましょう。
- 軸力(Nー図):働いてないので何も書かない
- せん断力①(Qー図):支点Aから点Dまで+5kN
- せん断力②(Qー図):支点Bから点Dまでー10kN
- 曲げモーメント①(Mー図):支点Aから点Dまで0から20の直線
- 曲げモーメント②(Mー図):支点Bから点Dまで0から20の直線
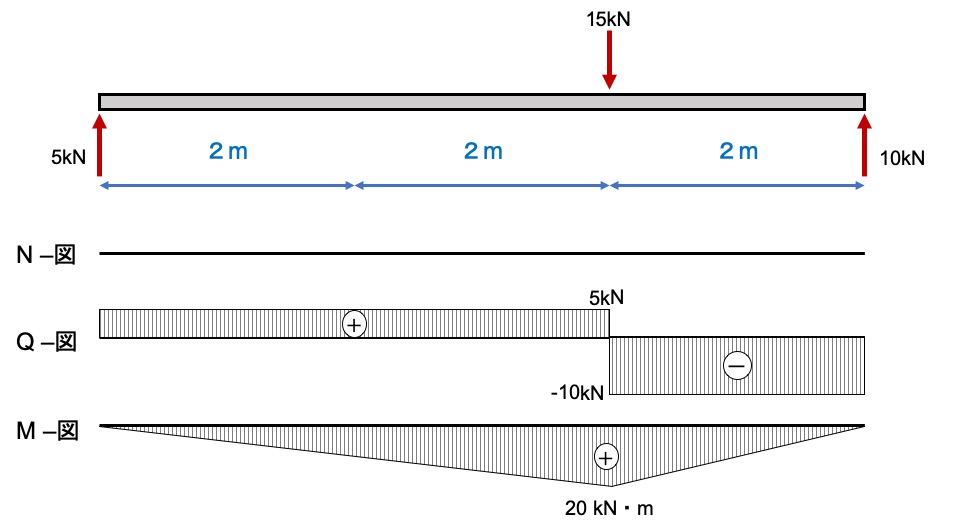

上の図のようになれば正解です!
断面力を求められると断面力図が書ける

断面力図も、力(荷重)の発生している点ごとに断面力を求めるだけで書くことができます。
難しく考えずに、力のつり合い式を解いていきましょう。
断面力図はこのように求めることができます。
- 支点反力を求める
- 端っこから力のある点ごとに区切る
- 断面力を求める
この記事を見た後にすべきことは問題をたくさん解くこと
この記事を見たあとはできるだけたくさんの問題を解きましょう。
手持ちの教科書や問題集でも構いません。
とにかくいっぱい問題を解きましょう。
それが、断面力図を理解するための近道です。
ちなみに、構造力学にオススメの参考書はこちら
たくさん問題を解いて、自分の力にして、構造力学の単位を取得しましょう!!!

