
断面2次モーメントがわかりません。
このままだとテストで点数取れません・・・
このような悩みを解決します。

明石高専で構造力学をちゃんと勉強した僕が解説します
この記事では、断面2次モーメントについて解説し、具体的な計算問題を一緒に解いていきます。
この記事を読みながら、実際の問題を解くことで、断面2次モーメントがわかるようになるはずです。
では、詳しく解説します。
目次
断面2次モーメントとは

断面2次モーメントとは、それぞれの座標軸に対して、任意の座標からの距離の2乗を部材の段面積で積分した量のことを言います。
特に、部材が曲げを受けるときの抵抗を求めたり、たわみや応力度の計算に必要になります。
とは言っても、この説明だとよくわからない呪文みたいですね。
図を見ながら、詳しく解説していきます。
断面2次モーメントの定義
断面2次モーメントは、『図心からの距離の2乗』×『微小な面積』の積分で表すことができます。
ある図形の中に、(テキトーに)赤枠で囲ったときの面積をdAと言う名前をつけます。
ある図形の真ん中(図心)を通る軸を考えます。この時の距離をそれぞれxとyとします。
この場合、断面2次モーメントは以下のような式で表すことができます。
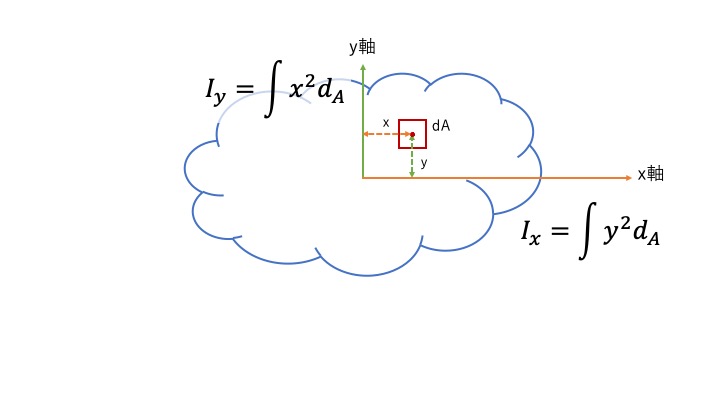

定義は、『こんなもんか』と流して大丈夫ですので、次に進みます。
断面2次モーメントの求め方
具体的な求め方について考えます。
- dAの正体を見破る
- 積分をとく
- 計算する
実は、簡単な3ステップで求めることができます。
では、一緒に計算してみましょう。
断面2次モーメントの公式
ここでは、基本的な3つの図形の断面2次モーメントを求めながら、計算方法を覚えていきましょう。
四角形の断面2次モーメント
以下の図で考えてみます。
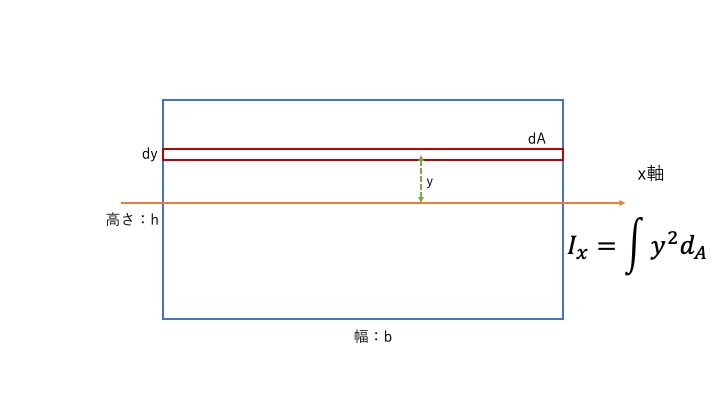
四角形の真ん中をx軸が通っているとします。
X軸に対して、断面2次モーメントを求めてみましょう。

このように四角形の断面2次モーメントが求められました。
三角形の断面2次モーメント
三角形も同じです。以下の図で考えてみましょう。
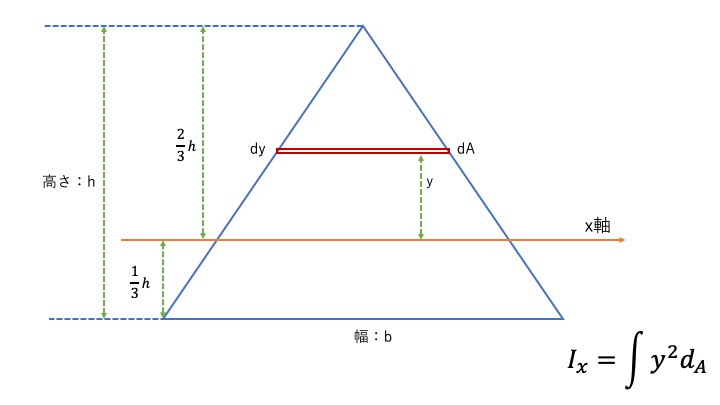
この場合のdAはy軸からの距離によって面積が変わりますね。
ここに注意して解いてみましょう。

円の断面2次モーメント
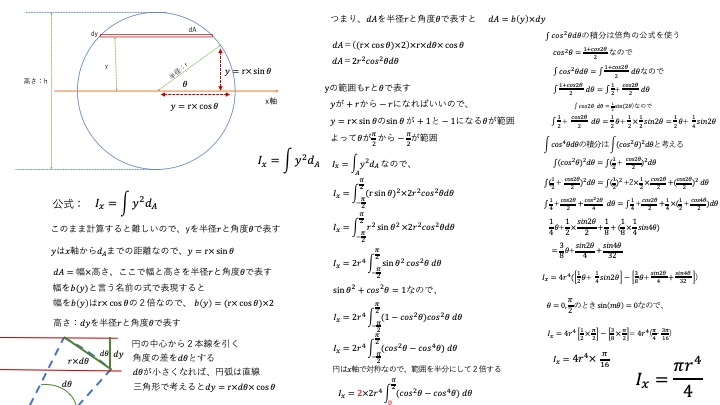
円は少し複雑です。以下の図で考えてみましょう。
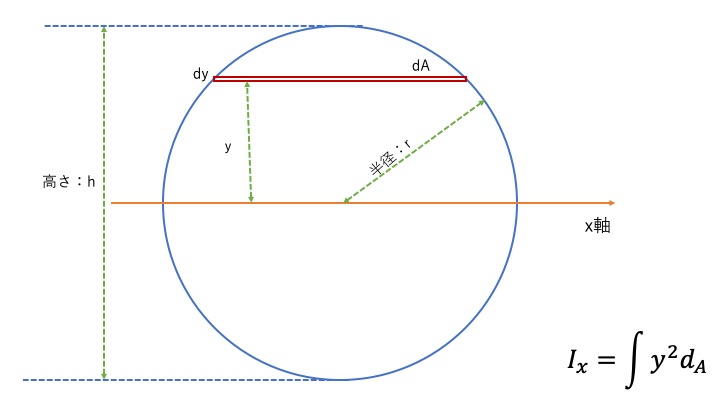
この場合、そのまま計算するとややこしいので、yを半径rと三角関数を使って表します。
x軸に対する断面2次モーメントが分かれば、底辺と高さを入れ替えて覚えよう
ここまで、x軸に対する断面2次モーメントを計算してきました。
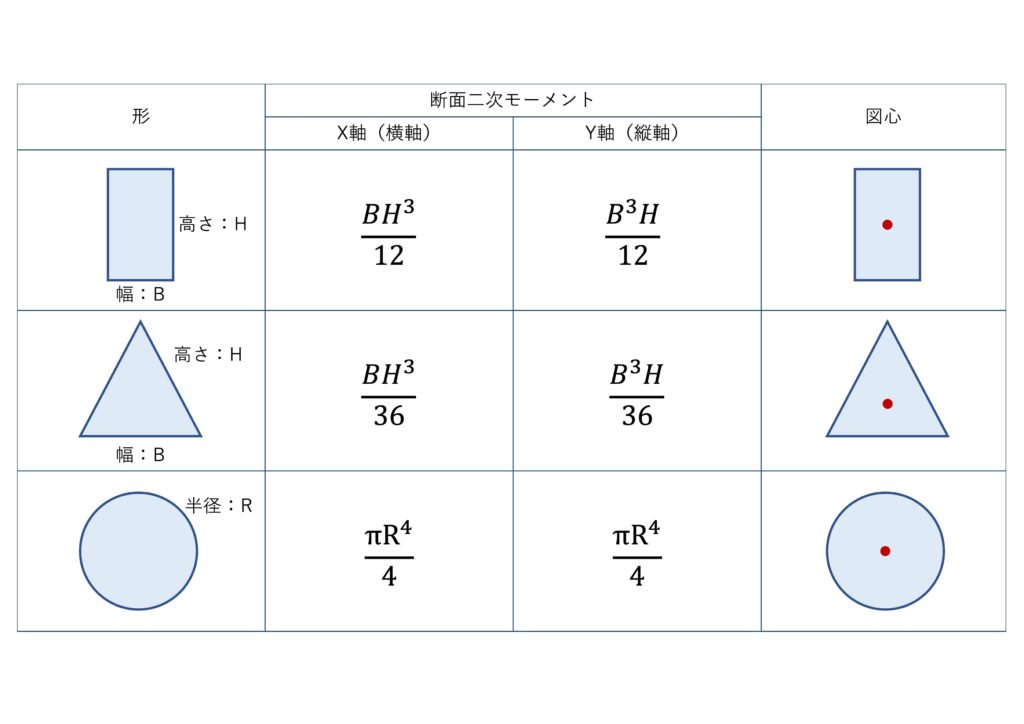
y軸に対する断面2次モーメントは高さと幅を入れ替えましょう。
では、一覧表を出しておきます。必要な時に見れるように保存しておいてくださいね。
軸から離れた断面2次モーメントの計算方法
今までは、図心がわかっている図形について計算をしてきました。
一方で、図心軸から離れた断面2次モーメントの計算は、ずれた分だけ調整すればOKです。
定義式は、『図心からの距離の2乗』×『微小な面積』の積分です。
『図心からの距離の2乗』にずれた分だけ足し算すればOKです。
『ずれ』を調整する=平行軸の定理
以下の例を計算してみましょう。

つまり、図心からずれた断面2次モーメントは以下の式で計算できます。
(図心を通る断面2次モーメントの2乗)+(図心からのずれの2乗×面積)
【参考】図心の求め方
図心の求め方は断面1次モーメントを使います。
つまり、断面1次モーメントを面積で割ったものが図心の位置になります。
図心の求め方や断面1次モーメントについては、『【断面一次モーメントとは】公式と図心の求め方をわかりやすく解説します』で詳しく解説しています。
複雑な形の断面2次モーメントの求め方
ここまでで、基本的な図形の断面2次モーメントと図心からずれた断面2次モーメントの計算(平行軸の定理)を解説しました。
この2つを利用すれば複雑な形の断面2次モーメントが計算できるようになります。
断面2次モーメントは合成(足し算・引き算)ができる
断面2次モーメントは合成(足し算・引き算)ができます。
なぜなら、簡単な図形に分解すればいいからです。
複雑な形でも、分解していけば基本的な形になります。
また、分解した図形の図心からのずれを1つずつ調整すれば複雑な図形の断面2次モーメントを求めることができます。
このように、断面2次モーメントは合成が可能です。
具体的な例を解説しますので、理解を深めていきましょう。
T字の断面2次モーメントの求め方
以下の図の断面2次モーメントを求めてみましょう。
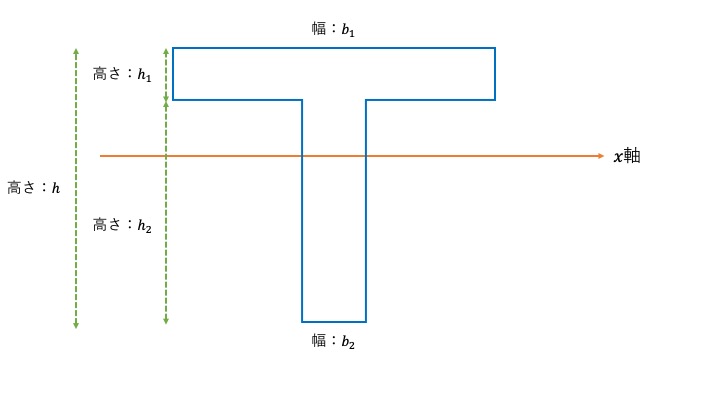
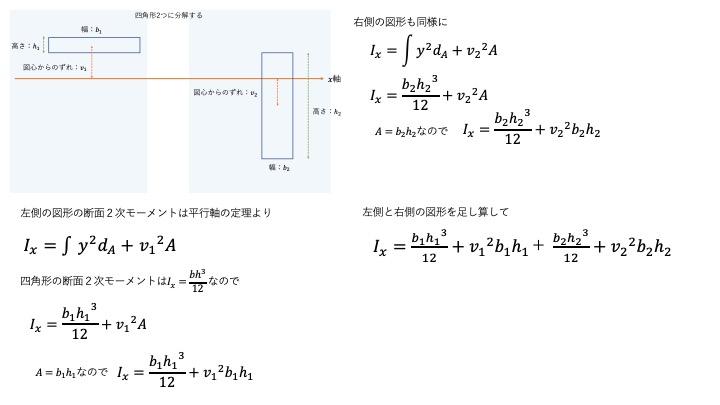
二つの図形に分解して、軸からのずれを調整します。
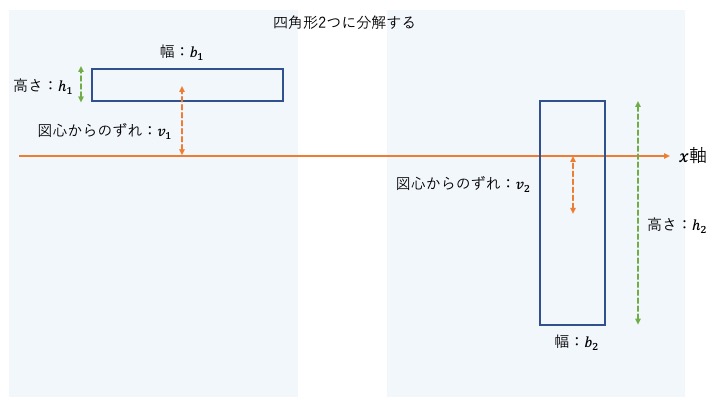
このようにすると解けます。
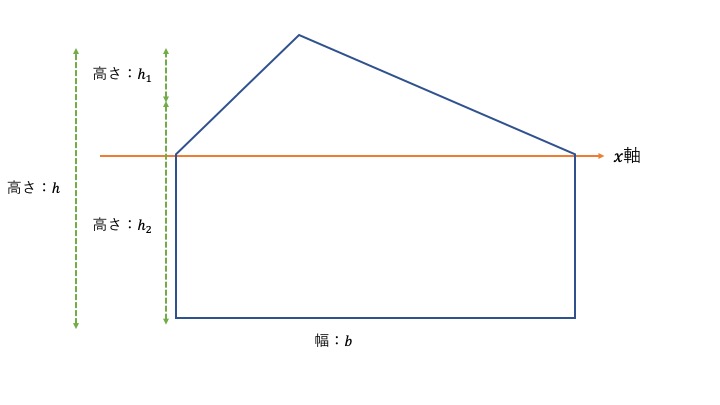
家形の断面2次モーメントの求め方
三角形と四角形が合わさったような図形も以下の通りに求めることができます。
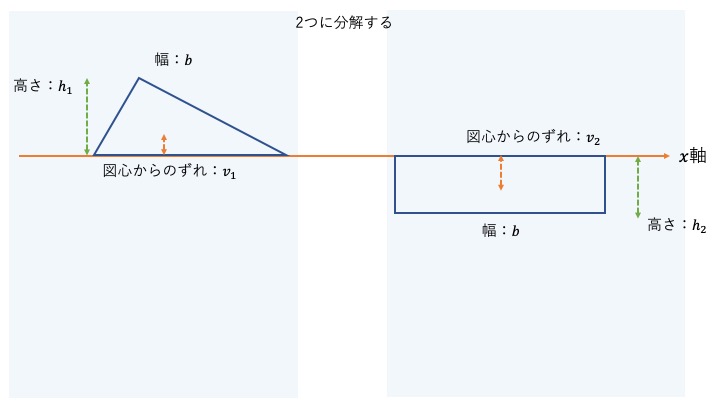
まずは図形を三角形と四角形の2つに分割しましょう。
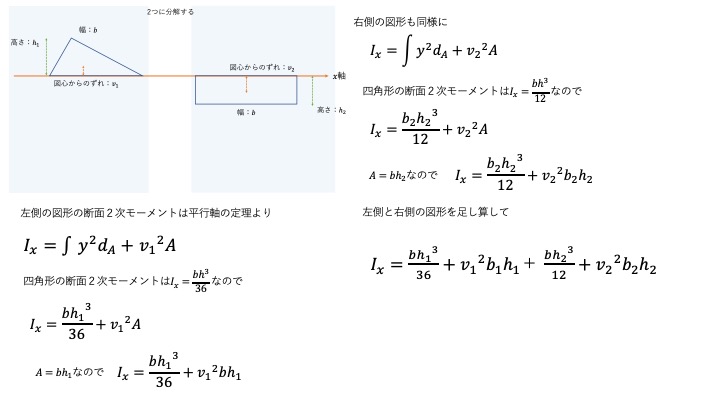
こうすると簡単ですね。三角形と四角形の断面2次モーメントと平行軸の定理を使えば、求めることができます。
中空(パイプ)の断面2次モーメントの求め方
ドーナツ型の断面2次モーメントも同様です。
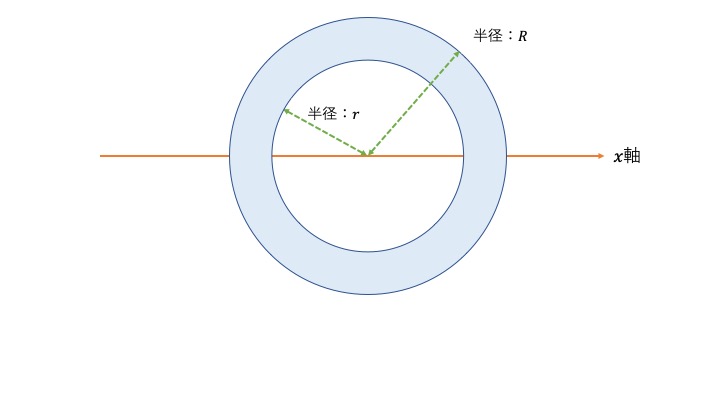
まずは2つの円に分けましょう。
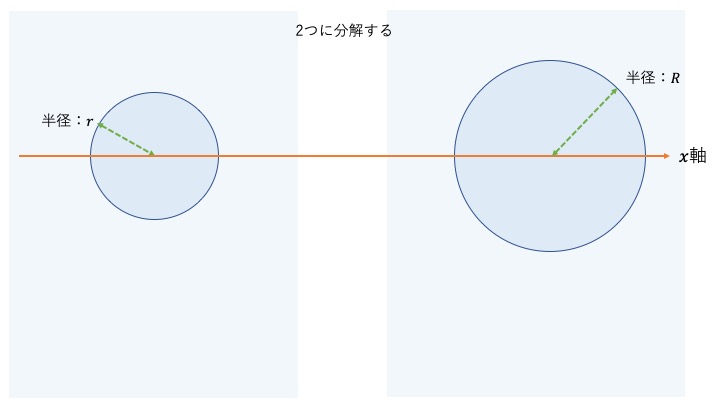
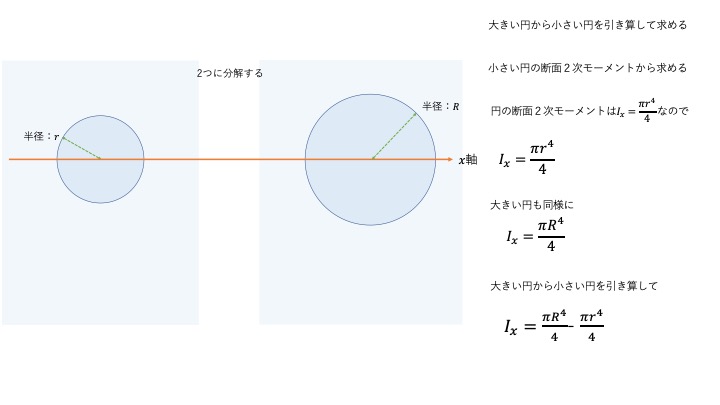
この場合は大きい円から小さい円を引くことで断面2次モーメントを求めることができます。
【まとめ】断面2次モーメントの計算方法

断面2次モーメントについて解説しました。
断面2次モーメントの求め方は以下の3ステップです。
- dAの正体を見破る
- 積分をとく
- 計算する
たったこれだけです。
この記事を見た後は『練習問題を解きましょう』
この記事を見ながら、基本ポイントがなんとなく理解できれば練習問題を解きましょう。
なぜなら、練習問題を解くことで断面2次モーメントをさらに理解しやすくなるからです。
練習問題を解いて、覚えることで解き方のパターンも身につきます。

教科書の問題集だと、難しくて解説なくてやる気が出ない・・・。
だったら、以下の問題集がオススメです。
いちばんやさしい建築構造力学問題集
また、『構造力学が苦手な人が読むべきオススメ参考書5選』では、構造力学全般にオススメの参考書を紹介してます。


