断面力の影響線の書き方がわかる【具体的な書き方を解説】

構造力学の影響線の書き方を解説します。影響線の書き方は以下の３ステップ

単純だけど難しいので、１つずつ解説していきますね。

明石高専の土木出身の僕が解説します。

構造力学の影響線の書き方を解説

影響線とは、『単位集中荷重を移動させたときのある点の断面力』です。

と言っても難しいので例題を解きながら理解していきましょう。冒頭にも書きましたが、影響線の解き方は以下の３ステップ

以下の図で解説します。

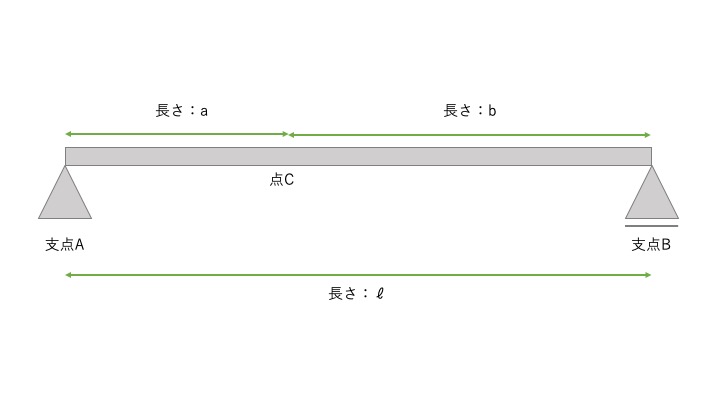
この時、単位集中荷重（P）が支点Aから\(x\)移動すると考えます。

影響線の書き方①支点反力を求める

支点反力を求めましょう。

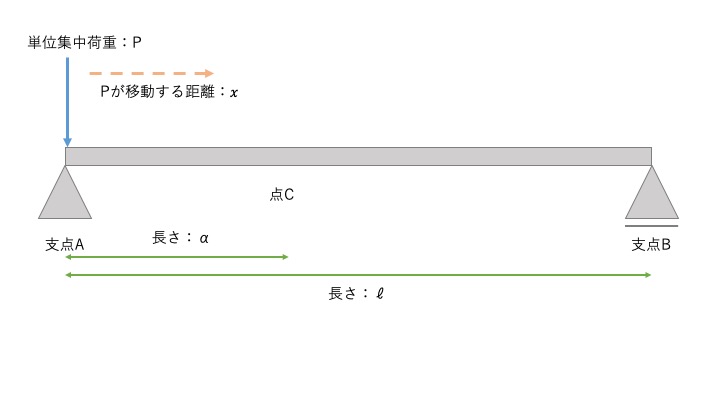
いっぱい考えても大変なので、基本的には以下の場所で考えてみましょう。

この例題の場合だと、支点A、支点B、点Cの３箇所で考えてみましょう。

支点Aの反力の影響線

単位集中荷重Pが支点A、支点B、点Cにいる時の支点Aの反力\(V_{A}\)を考えてみましょう。

単位集中荷重が点Cに移動したときは、支点Bを基準にモーメントを使って解きましょう。

\( V_{A} \times \ell = P \times (\ell$ - a)\)

この時\(P=1\)なので、\( V_{A}= 1- \dfrac{a}{\ell} \)

では、\(aがxの時\)だったら、\( V_{A}= 1- \dfrac{x}{\ell} \)です。図に書くとこんな感じ。

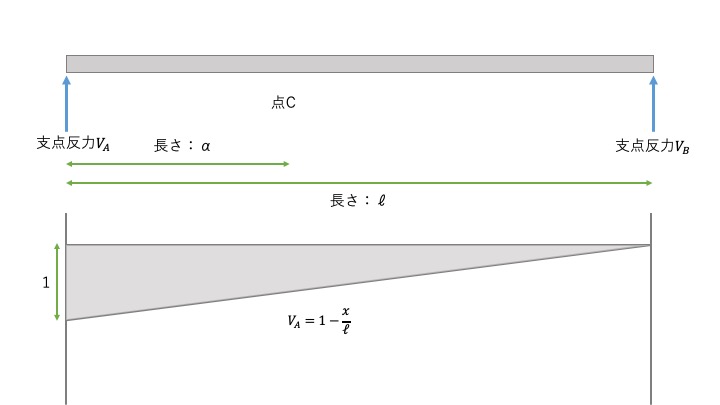
支点Bの反力の影響線

同じように考えます。

支点Aを基準にモーメントを考えます。

\( V_{B} \times \ell = P \times a\)

この時\(P=1\)なので、\( V_{B}=\dfrac{a}{\ell} \)

では、\(aがxの時\)だったら、\( V_{B}= \dfrac{x}{\ell} \)です。図に書くとこんな感じ。

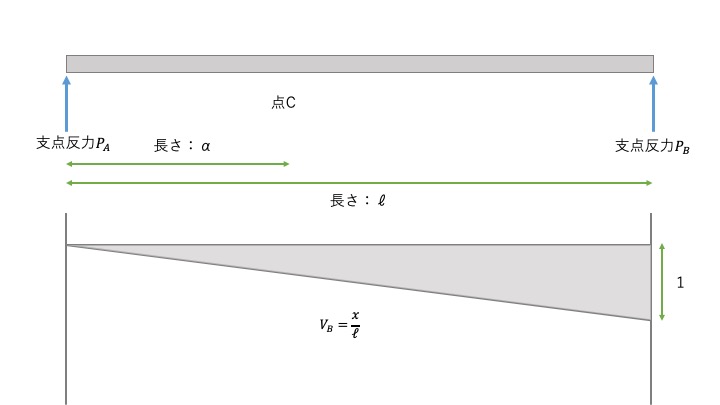
影響線の書き方②せん断力の影響線の書き方

この図で点Cのせん断力の影響線を考えます。

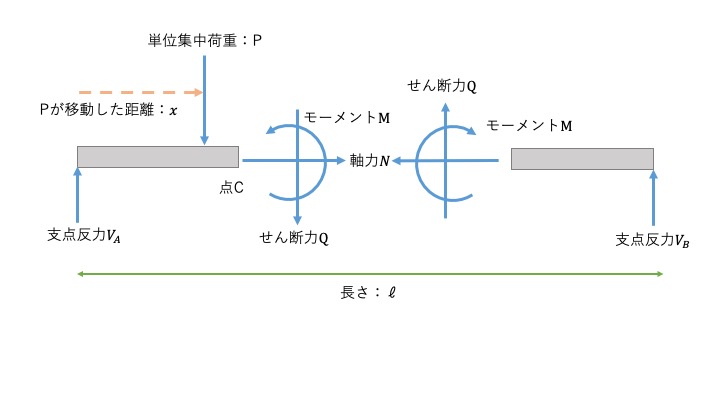
この時のせん断力の影響線は以下の２つを考えます。

単位集中荷重が点Aから点Cにあるとき

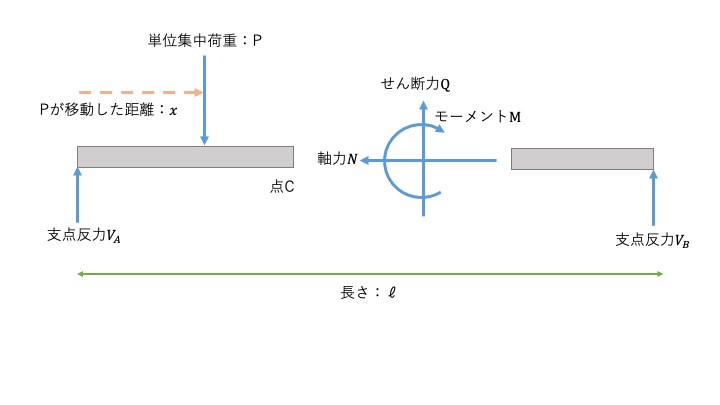
この時のつり合い式も、\( V_{A} = P + Q \)

\(V_{A} = 1-\dfrac{x}{\ell}\)なので、

\(1-\dfrac{x}{\ell} = P+Q\)、\(P=1\)なので、

\(Q = -\dfrac{x}{\ell}\)

単位集中荷重が点Cから支点Bにあるとき

この場合、以下の図のようになります。

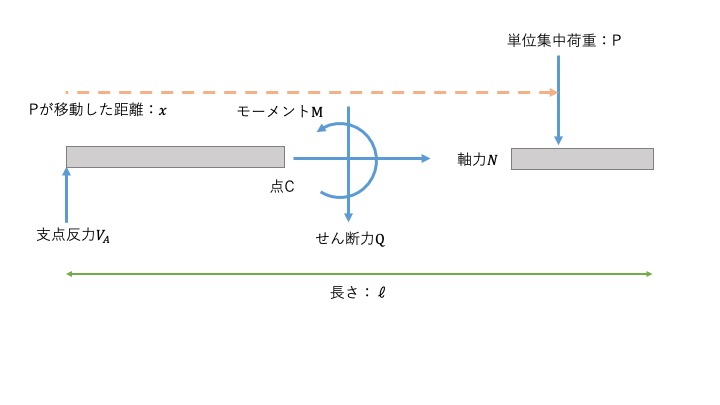
点Cより左側だけでつり合い式を考えると、\( V_{A} =Q\)

この場合、\(V_{A}= 1 - \dfrac{x}{\ell}\)なので、

\(1 - \dfrac{x}{\ell} = Q\)

つまり、点Cを基準に以下のような式になります。

つまり、点Cのせん断力の影響線は以下になります。

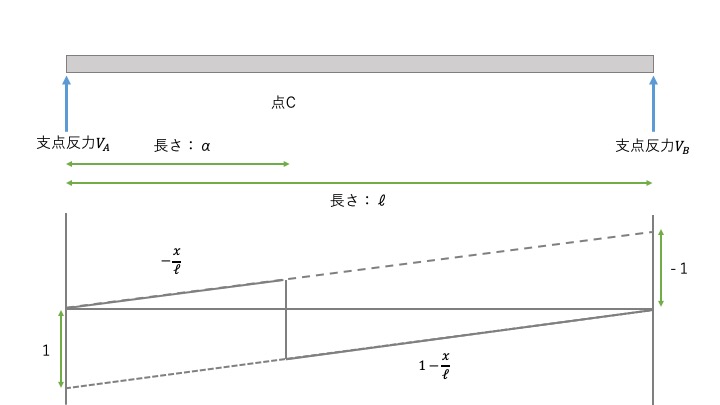
影響線の書き方③曲げモーメントの影響線の書き方

せん断力と一緒です。以下の２つの場合を考えます。

単位集中荷重が点Aから点Cにあるとき

単位集中荷重が支点Aから点Cにあるときは、右側で考えましょう。

つり合い式は\( M = V_{B} \times b \)

\( V_{B} = \dfrac{x}{\ell} \)なので、

\( M = \dfrac{x}{\ell} b \)

単位集中荷重が点Cから支点Bにあるとき

今度は、部材の左側で考えましょう。

つり合い式は\( M = V_{A} \times a \)

\( V_{A} = 1 - \dfrac{x}{\ell} \)なので、

\( M = (1- \dfrac{x}{\ell})a \)

影響線を書くとこうなります。

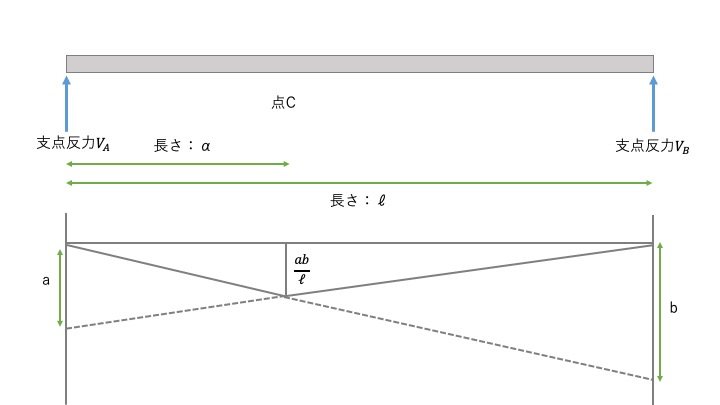
これで、影響線が完成しました。

まとめ：断面力の影響線の書き方

影響線の書き方は以下の通り

構造力学は問題を解いて覚えよう

構造力学は問題を解いて理解していきましょう。

構造力学にオススメの参考書は以下でまとめています。