分布荷重は集中荷重に置き換えよう【計算方法は面積を求めるだけ】

分布荷重は集中荷重に置き換えて考えましょう。

この記事を見ながら一緒に分布荷重を理解していきましょう。

分布荷重は集中荷重に置き換えよう

分布荷重の解き方は以下の通り

この２つだけ。簡単ですね。詳しく解説します。

分布荷重が四角形の場合

分布荷重が四角形の場合を考えてみましょう。

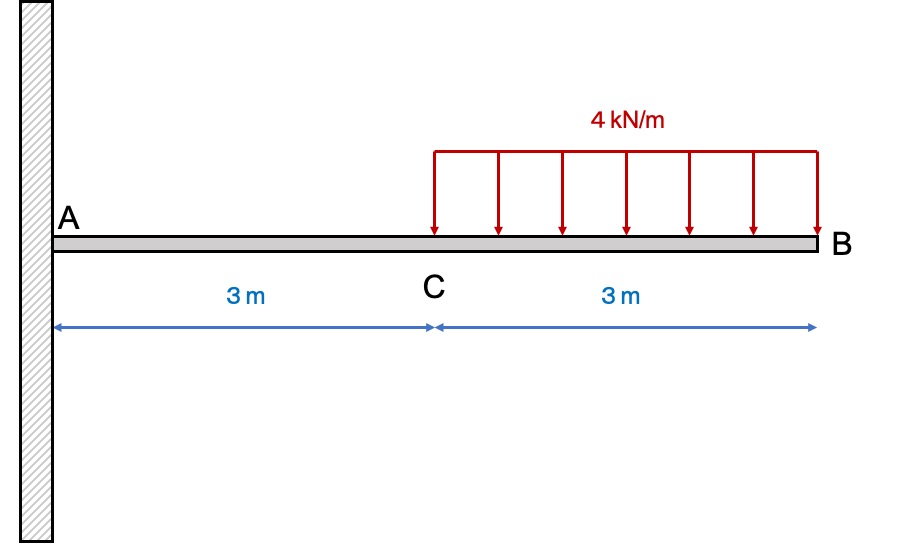
この場合の分布荷重は次のように考えます。

分布荷重の大きさ

この場合は、\(4kN/m\)の荷重が\(3m\)かかっているので、

\(4kN/m \times 3m = 12kN\)です。

分布荷重を集中荷重に置き換えた時の位置

四角形の場合、分布荷重の真ん中になります。

つまり、点Bから左に1.5mの位置の集中荷重に置き換えることができます。

分布荷重が三角形の場合

分布荷重が三角形の場合を考えてみましょう。

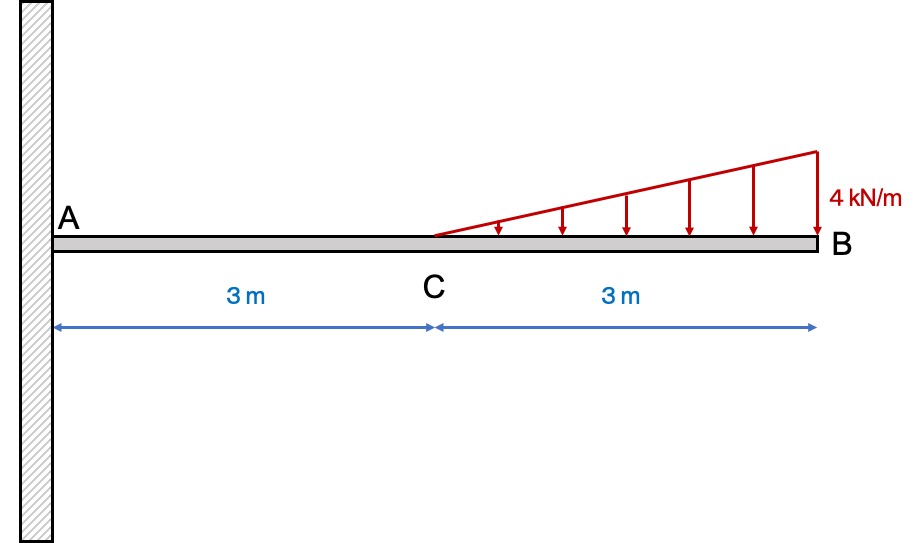
注意することは『重心の位置』です。

分布荷重の大きさ

三角形の面積を求めればいいので、

\( 4kN/m \times 3m \times \dfrac{1}{2} = 6kN \)

荷重の位置

三角形の重心の位置は底辺から\( \dfrac{1}{3}\)の位置です。つまり、点Bから1mの位置

三角形の重心の位置の求め方は断面1次モーメントを使います。『【断面一次モーメントとは】公式と図心の求め方をわかりやすく解説します』で詳しく解説しています。

図で書くとこうなります。

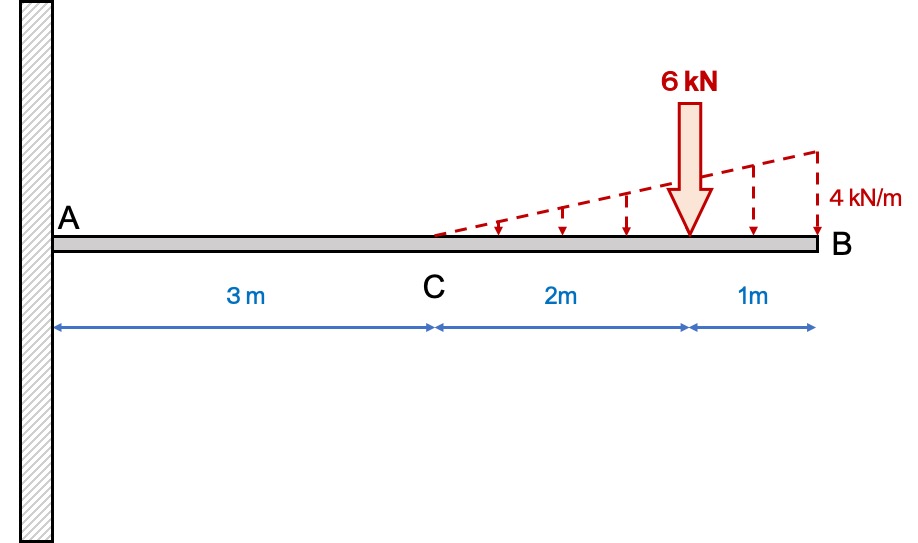
【例題】三角形の分布荷重から断面力を求めてみよう

固定端の先端に三角形の分布荷重が働いているはりの断面力を求めてみましょう。

三角形の分布荷重の計算も簡単です

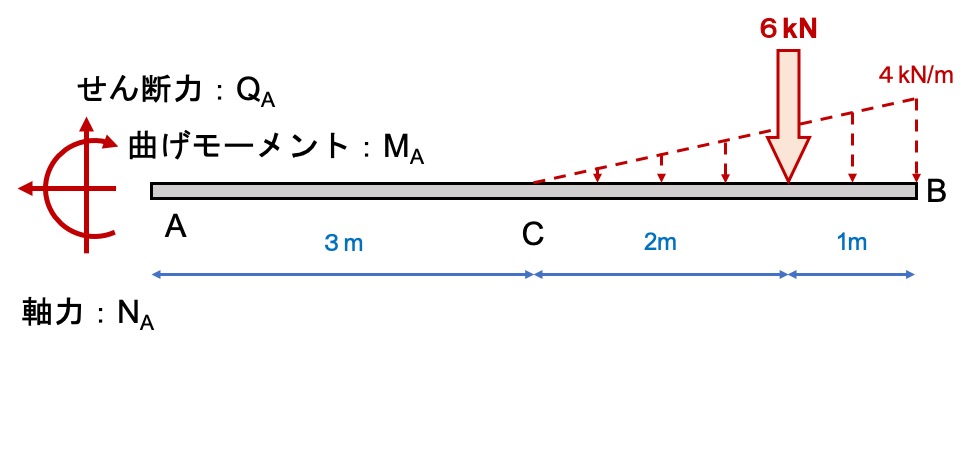
さっき求めた分布荷重から、支点反力を求めましょう。

支点反力の求め方は『支点反力の求め方をわかりやすく解説します【縦と横に分解しましょう】』で詳しく解説しています。

支点反力がわかったら断面力を求めてみよう

C点で仮想的に切断して、断面力を求めます。

断面力の求め方は『【断面力とは】断面力の求め方や応力との違いを解説』で詳しく解説してます。

C点のせん断力

C点の曲げモーメント

三角形の分布荷重がかかる固定端のはりの断面力図を書いてみよう

では、断面力図を書いてみよう。

断面力図の書き方は『断面力図の書き方は簡単【やることは３つだけ】』で詳しく解説してます。

断面力図は荷重のかかるところで分けて考えよう

断面力図の書き方のコツは荷重のかかる位置で分けて考えることです。

支点Aから点Cまで

抜き出して書くとこんな感じ。

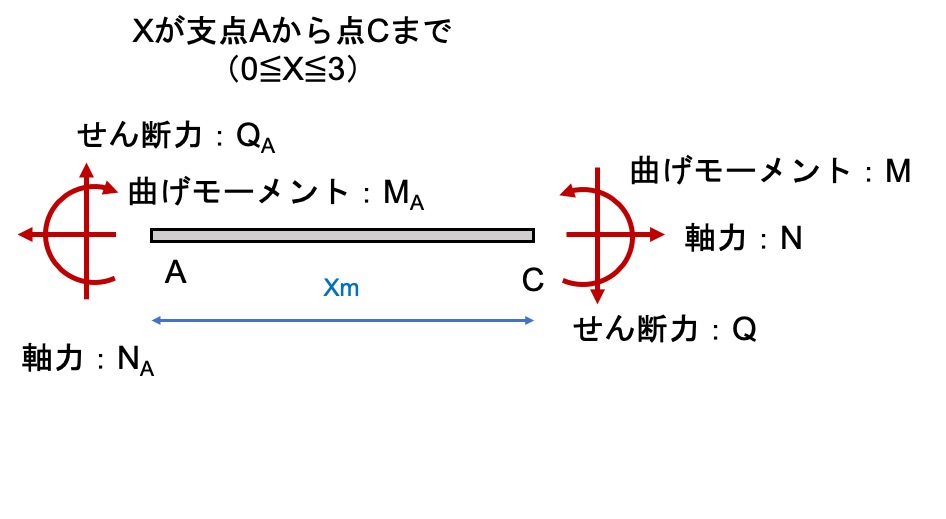
こんな図を見ても慌てないで、１個ずつ考えよう。

軸力

せん断力

曲げモーメント

支点Aから支点Bまでの断面力を考えてみる

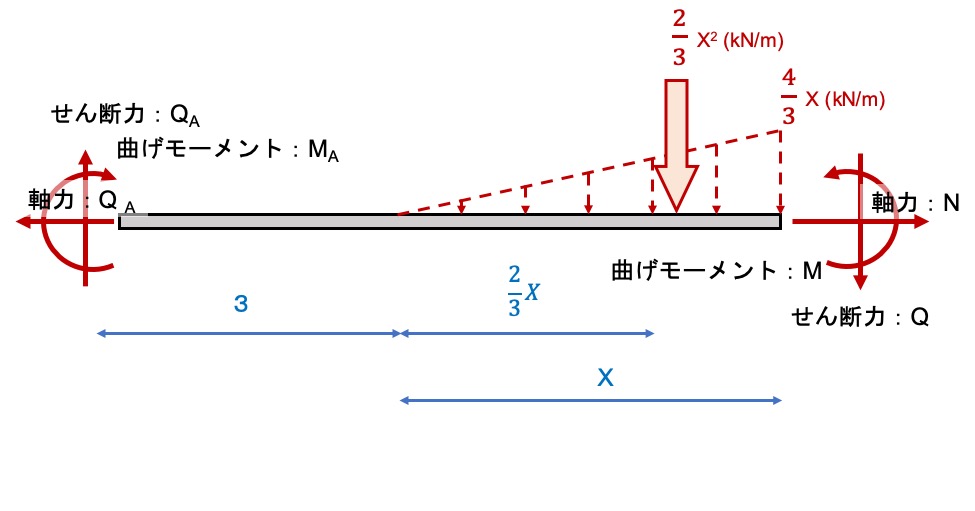
Xの向きを揃えた方が計算しやすいので、上の図になります。

この図でもやることは一緒。

１個ずつ落ち着いてときましょう。

三角形分布の傾きは３mで４kN/mなので、Xを使うと次のようになります。

これを高さに見立てて、底辺Xの三角形の面積は、次のようになります。

先ほど求めたC点の断面力と断面力図の求め方を組み合わせて考えましょう。

軸力の断面力図

せん断力の断面力図

せん断力はXの値に従って変化します。

上向の力を左辺・下向きの力を右辺にすると

Q_A=2X²/3+Q

つまり、次の式になります。

X＝３にする（点B）では０になりますね。

曲げモーメントの断面力図

曲げモーメントもXの値にに従って変化します。

Xの位置を中心に、右回りの力を左辺・左回りの力を右辺にすると

M+(2X²/3)×X/3＋M_A=+Q_A×(X+3)

＊QA（支点反力）は（X＋３）mの位置にあることに注意です！

つまり、曲げモーメントはこうなります。

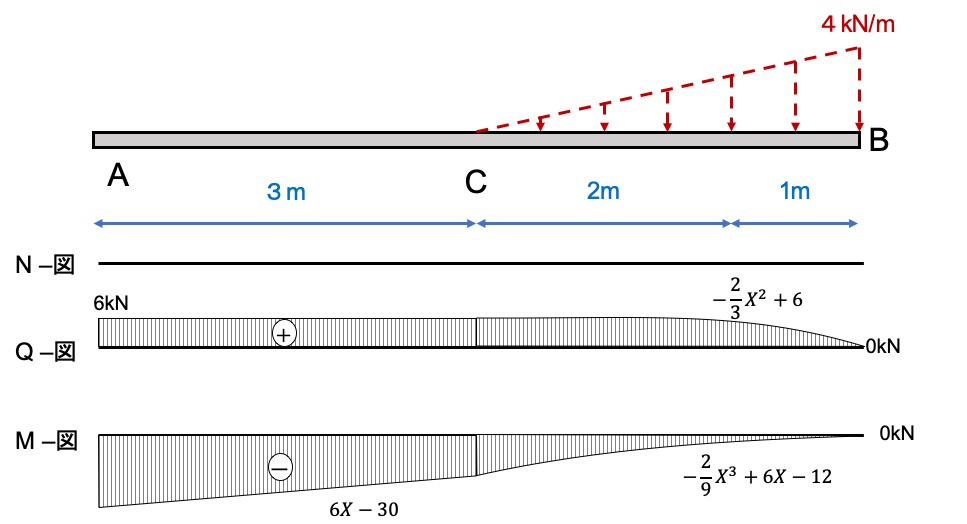
断面力図を書いてみる

ここまで求められたら、図を書いてみましょう。

まとめ：分布荷重は集中荷重に置き換えて計算しよう

分布荷重のまとめです。

これだけわかれば完璧です。

構造力学が苦手だなって思うなら問題を１問でも多く解きましょう。

優しくて簡単でおすすめの問題集はこれ。

他にも、構造力学におすすめの参考書、問題集は『構造力学が苦手な人が読むべきオススメ参考書5選』でまとめています。