
構造力学にも微分方程式でてくるの?
勘弁してよ。
構造力学シリーズも難しくなってきました。
今回は、『微分方程式』を使って『たわみ』を解いてみましょう。

たわみの解き方はこれだけじゃないので・・・
こんな解き方もあるんだなーと覚えておきましょう。
今回も、基礎知識を押さえながら、テストで使えるテクニックを紹介していきます。

3分ほどで読める内容にしていますので、一緒にやってみましょう!
目次
構造力学のたわみを微分方程式を使った求め方をわかりやすく解説

『たわみ』とは

ところで、『たわみ』って何?

ほら、定規を曲げた時のアレです。

(・・・アレってなんだよ。)
身近なもので言うと、まっすぐな定規を曲げると”湾曲”しますよね。
それがたわみです。
あなたは、薄い板の上を歩いたことがありませんか?
真ん中に行くほど『たわみ』は大きくなっていき、同時に恐怖感を感じますよね。
この『たわみ』を微分方程式で求めていきましょう。
微分方程式で『たわみ』を解くための3つのポイント

構造力学もそうなんだけど、微分方程式も苦手なんだよね。

こんな本がありますよ。
会話調で読みやすく、レビューも高いのでおすすめです!
『たわみ』を微分方程式で解くためには3つのポイントがあります。
- 反力を求める
- 曲げモーメントを求める
- 微分方程式を解く

ひとつずつ見ていきましょう!
微分方程式で解くたわみ①支点反力を求める
構造力学の基礎。まず初めに支点反力を求めましょう。
支点反力の求め方はこちら

微分方程式で解くたわみ②曲げモーメントを求める
支点反力が求められたら、次は曲げモーメントを求めましょう。
断面力図を書くときに求めますよね。
曲げモーメントの求め方はこちら
https://www.betterkiso.com/mechanics/structural/section-force-diagram-of-beam/微分方程式で解くたわみ③微分方程式を解く

で、、でた、微分方程式。

詳しいことは学校の先生に任せて、テストに出るところだけ解説しますね。
ここで、たわみについて下の図を見てみましょう。
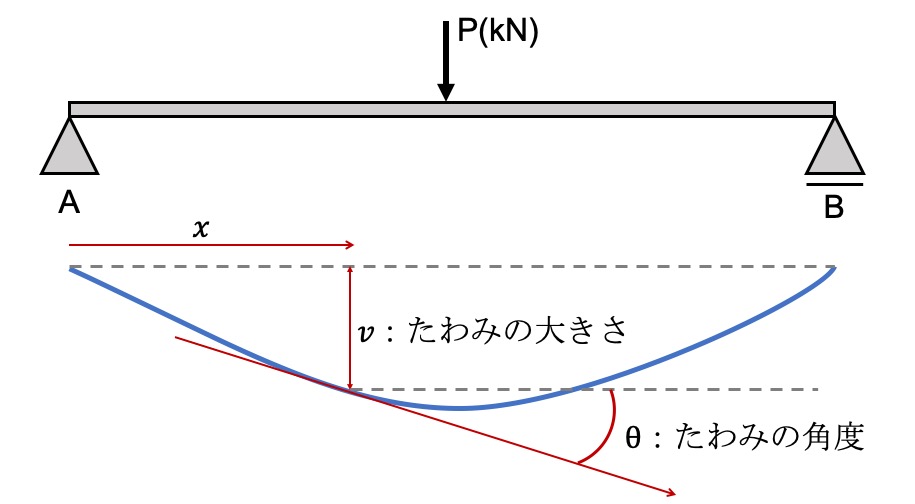

図で言うと、『vとθを求めましょう』と言う問題です。
『たわみ』を求める微分方程式は次の式です。
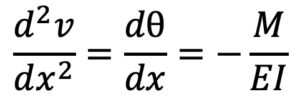
ここで、
- V:たわみの大きさ
- θ:たわみの角度
- M:曲げモーメント
- E I:曲げ剛性(どれだけ曲げにくいか)

丸暗記してもいいと思います。
覚え方は、たわみを2回微分すると、マイナス(曲げモーメント/曲げ剛性)

そのままやん。
でも、こんなのどうやって解くの?
文章だけではわからないので、一緒に問題を解いてみましょう。
微分方程式を使った『たわみ』の解き方(具体例)
今回は、次のはりのたわみを求めていきます。
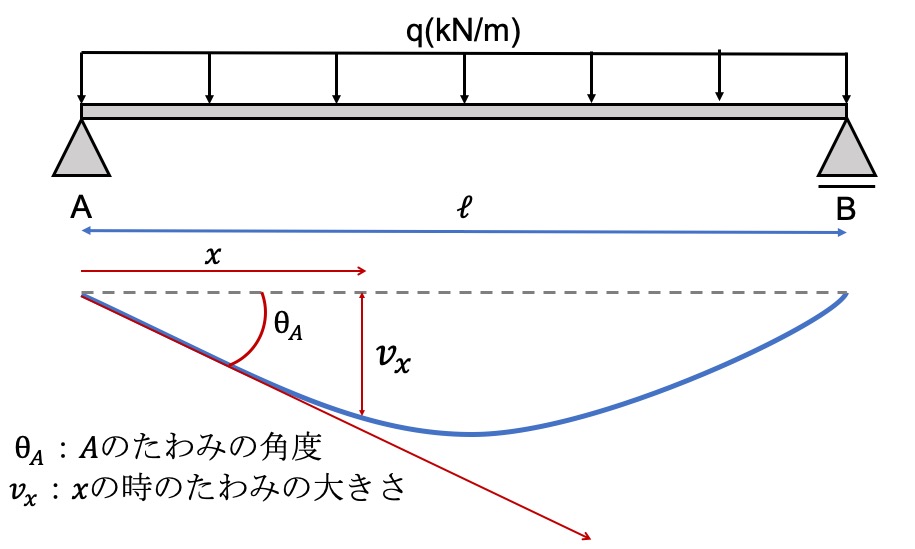
支点反力と曲げモーメントを求める
上の記事で紹介している通りですが、簡単に計算していきます。
支点反力は次の式で求められます。
VA+VB=qℓ
qℓ/2=VBℓ
VA=VB=qℓ/2
曲げモーメントは次の式で求められます。

支点Aを中心に曲げモーメントを考えてみよう。
Mx+VBℓ=qx2/2
Mx=(qℓx/2)-(qx2/2)

ここまでは過去の記事でやりましたね。
微分方程式を使って『たわみ量』『たわみ角』を求める
それでは、先ほどの微分方程式を使って『たわみ』『たわみ角』を求めてみましょう。
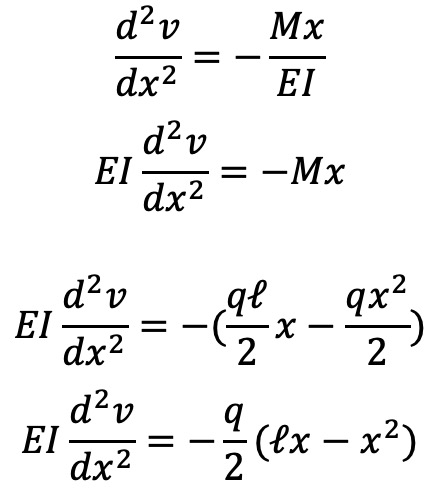
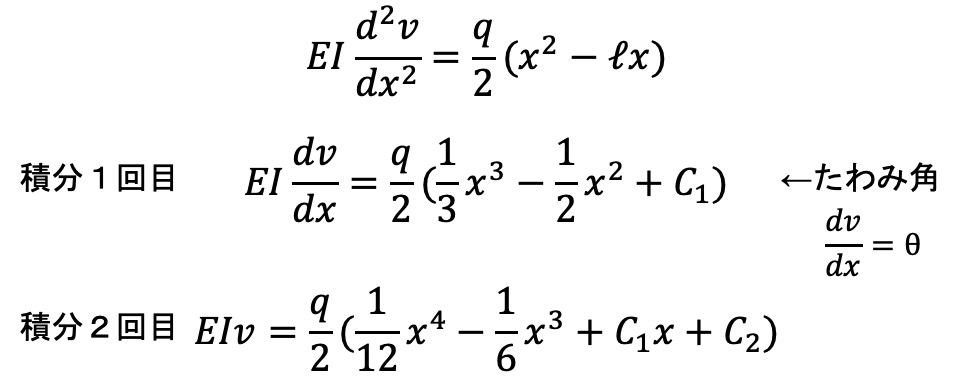

あれ?Cってなんですか?

積分定数ですね。次の条件で解くことができます。

境界条件?
微分方程式を解くためには、積分定数を求めないといけません。
積分定数を解くためには、次の条件(境界条件)を使うことができます。
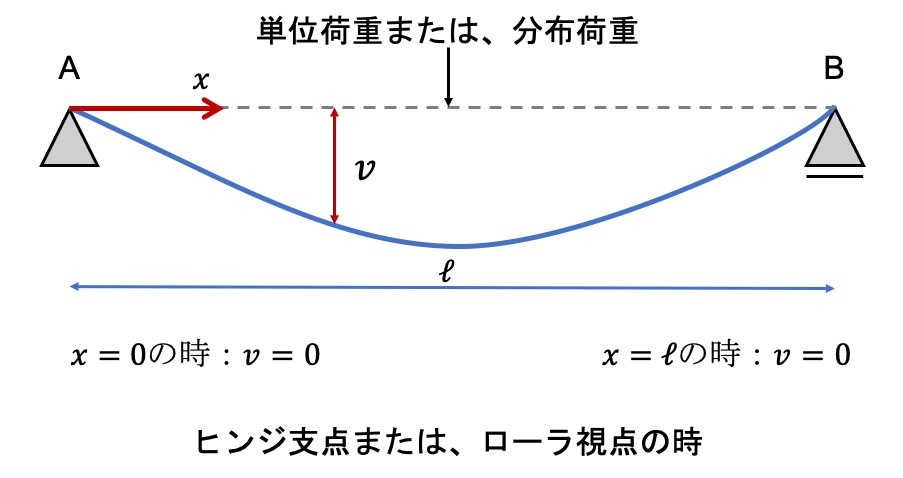
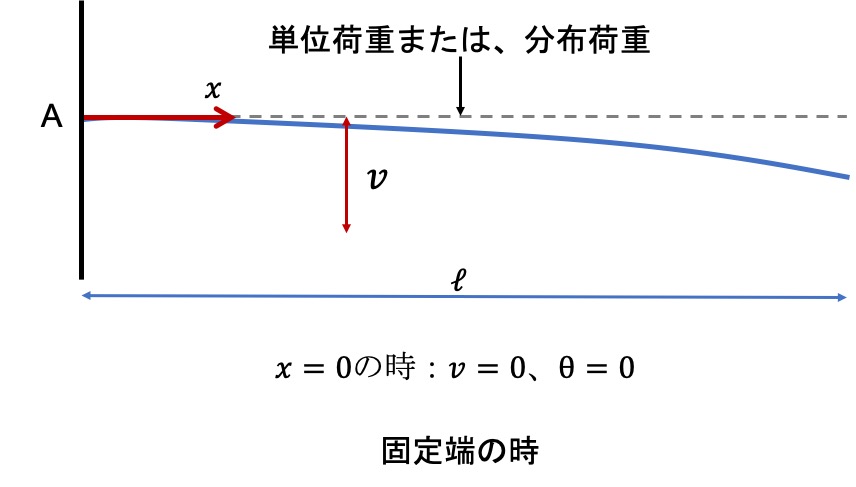

今回は、ヒンジ支点・ローラ支点の場合なので、
x=0の時:たわみ=0、x=ℓの時:たわみ=0でいきましょう。
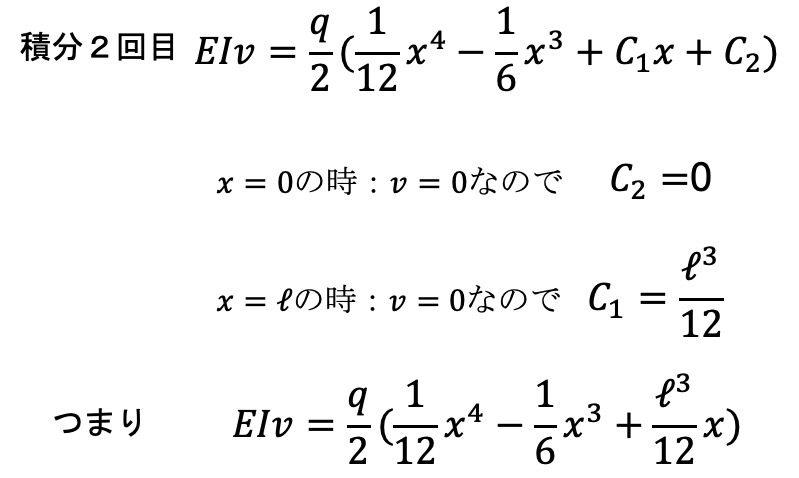

上の式がxの時のたわみ量です。
支点Aの時のたわみ角を求めてみましょう。
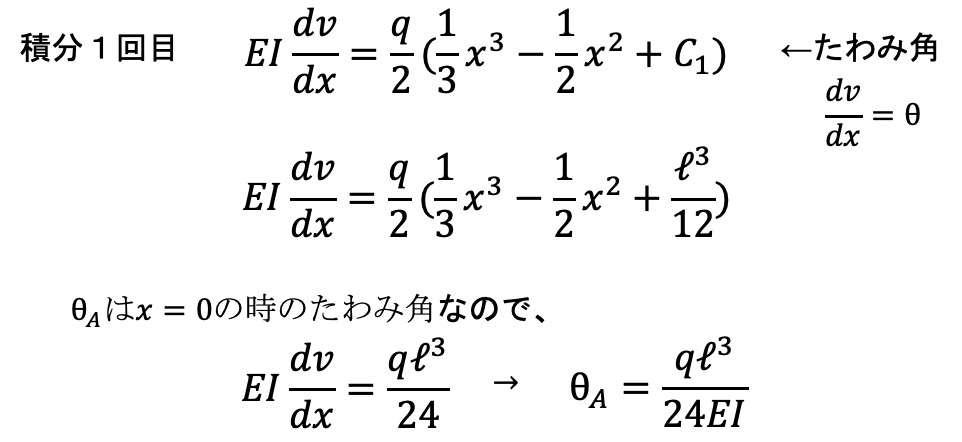
以上で求められました。
【まとめ】微分方程式を使った『たわみ』『たわみ角』の求め方
まとめです。
- 支点反力を求める
- 曲げモーメントを求める
- たわみの微分方程式を求める
- 境界条件を代入する

むずかしく思える微分方程式もひとつずつ解いていけばシンプルですね。
この記事を読んだ次は、問題を解いて慣れていきましょう。

記事を読むだけでは、内容まで理解できません・・・
実際の問題にたくさん解いて慣れていきましょう。
- 3つの力学が一つの冊子になっている
- 丁寧な図解と解説がある
- 幅広い問題があり公務員試験にも使える
構造力学の演習はもちろん、土質力学と水理学の演習もこの1冊で十分です。

3つの科目の演習と詳しい図解と丁寧な解説が入って4000円でお釣りがきます。
これこそ高コスパ。
テストで点数を取るためには問題をたくさん解いて計算に慣れていくことがとても大切です。
以上、とたんでした



