構造力学や材料力学を学ぶ上で、避けて通れないのが断面一次モーメントの計算ですね。この概念は非常に抽象的で分かりづらく、「公式は知っているが、T字型やI型の複雑な断面の計算方法が分からない」「そもそも何のために計算するのか」と悩む方も多いのではないでしょうか。
安心してください。
この記事では、断面一次モーメントの「意味(定義)」から、長方形・T字型・I型断面など実務で遭遇するあらゆる形状の具体的な計算手順までを、ステップバイステップで完全解説します。
この記事を読み終える頃には、あなたは図心を正確に求め、あらゆる断面の断面一次モーメントを自信を持って計算できるようになっているでしょう。
目次
断面一次モーメントとは?(定義・意味・単位)
構造力学を学ぶ上で、断面一次モーメントが抽象的で分かりにくいと感じる方は多いでしょう。
ここでは、難しい数式を避け、まず「この値が構造物の中で何を意味しているのか」という本質的な部分を理解しましょう。この定義の理解が、正確な計算への第一歩となります。
断面一次モーメントの定義と意味(何を表すのか)
断面一次モーメントとは、断面内の微小な面積と、その面積の基準軸からの距離を掛け合わせたものを、断面全体で合計した値です。
【意味:最も簡単に言うと】
断面一次モーメントは、「断面の偏り(ばらつき)」を示す指標です。この値は、特にせん断応力(構造物をズレさせようとする力)を計算する際に不可欠な要素となります。
- 公式: \(S =A \times y_{G}\) (ここで \(A\) は断面の全断面積、\(y_{G}\) は基準軸から図心までの距離)
まずはこのシンプルな公式で計算できることを理解し、具体的な応用に進みましょう
断面一次モーメントの公式と単位
断面一次モーメントの単位は、長さの3乗で表されます。
- 単位: \(cm^{3}\) または \(m^{3}\)
- 理由: 公式 \( S =A\times y_{G}\) において、面積 \(A\) は\(cm^{3}\) 、図心までの距離 \(y_{G}\) は \(cm \)であり、これらを掛け合わせるためです。
【補足】積分による導出について
断面一次モーメントは本来、積分 \(S = \int yd_{A}\) によって定義されます。理論的な背景(なぜ \(S = \int yd_{A}\) が \(Ay_{G}\)になるのか)について深く学びたい方は、断面一次モーメントの基本図形の導出をご覧ください。
断面一次モーメントが「ゼロ (0)」になる条件
断面一次モーメントは、基準軸の選び方によって値が変わるという特徴があります。特に重要な性質として、以下の条件を覚えてください。
- 条件: 断面一次モーメントは、「図心(重心)を通る軸」に関して計算すると、その値は必ずゼロ (0) になります。
- 応用: この性質は、後に複雑な断面の図心の位置を求めるための基本原理として使われます。「断面一次モーメント = 0」になる場所が、その断面の重心(図心)である、という認識を持ちましょう。
断面一次モーメントの基本的な求め方(長方形・三角形)
抽象的な定義を理解したところで、実際に手を動かして計算してみましょう。複雑な断面も、最終的にはこの長方形や三角形の集合体として扱います。まずはシンプルな図形で、計算手順を確実にマスターしてください。
断面一次モーメント計算の基本ステップ
複雑な断面一次モーメントや図心を求めるために、常にこの3ステップを徹底してください。
- 基準軸の設定: 計算を始める前に、断面の最下端など、分かりやすい位置に基準軸(X軸)を明確に設定する。
- 図形の分割: 複雑な断面を、長方形や三角形など、図心位置が既知のシンプルな図形に分割する。
- 部分の計算と合計: 分割した各図形ごとに断面一次モーメントを計算し、それらを合計する。
例題1:長方形断面の断面一次モーメントの求め方

底辺を基準軸にしましょう。
\(G_{x}=A \times y_{G}\)なので、
\(G_{x}=bh \times \frac{h}{2}\)
これを計算すると\(G_{x}=\dfrac{bh^{2}}{2}\)となります。
y軸も同じように考える
\(G_{y}\)も同じように考えると、\(G_{y}=A \times x_{G}\)
\(G_{y}=hb \times \frac{b}{2}\)
これを計算すると\(G_{y}=\dfrac{b^{2}h}{2}\)となります。
例題2:三角形断面の断面一次モーメントの求め方
では、三角形もやってみましょう。
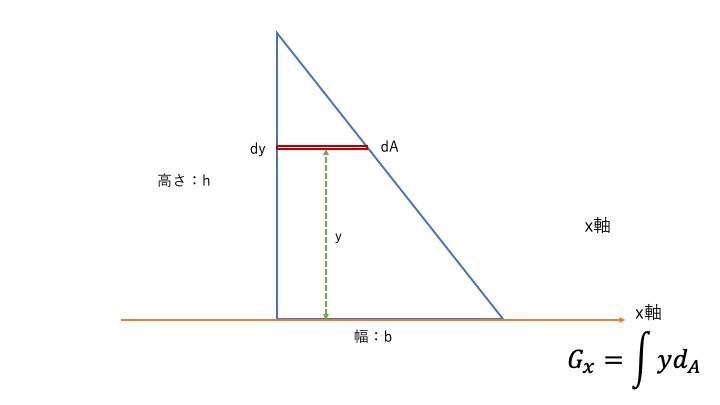
底辺を基準軸にしましょう。
\(G_{x}=A \times y_{G}\)なので、
\(G_{x}=bh \div 2 \times \frac{h}{3}\)
これを計算すると\(G_{x}=\dfrac{bh^{2}}{6}\)となります。
y軸も同じように考える
\(G_{y}=A \times x_{G}\)なので、
\(G_{y}=hb \div 2 \times \frac{b}{3}\)
これを計算すると\(G_{y}=\dfrac{hb^{2}}{6}\)となります。
円の断面一次モーメント
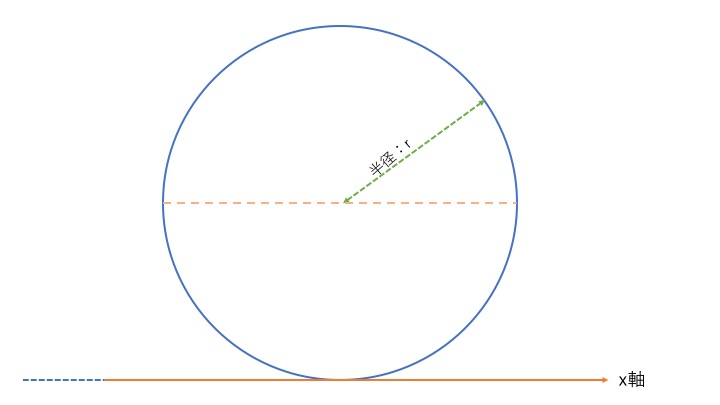
円も同様に考えましょう。
\(G_{x}=A \times y_{G}\)なので、
\(G_{x}=\pi r^{2} \times {r}\)
\(G_{x}=\pi r^{3}\)
基本的な図形の断面一次モーメントと図心の導出は、断面一次モーメントの基本図形の導出で解説していますので詳しく知りたい方は参考にしてください。
複雑な形状(T字、I字)の断面一次モーメントと図心の計算
構造部材の断面は、H型鋼やT字型など、長方形の組み合わせで構成されていることがほとんどです。これらの複雑な形状の計算は、図心(重心)を正確に求めることから始まります。
複雑な図形の図心の求め方(公式と手順)
複雑な図形の図心(重心)の位置 \y_{G} は、断面一次モーメントの総和と断面積の総和を用いて求められます。
図心の公式
\(frac{\sum G}{\sum A}= \frac{\sum A_{i} \times y_{Gi}}{\sum A}\)
まず基準軸に関して \(sum G\) を計算すれば、後は総断面積 \(sum A\) で割るだけで図心が得られます。
T字型断面の断面一次モーメントと図心
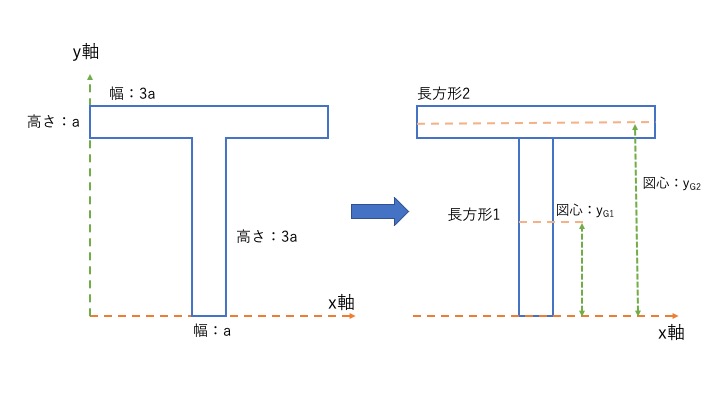
T字でもやることは同じ。簡単に計算するために長さは全てaで統一しています。
まずは、T字を図のように長方形1と長方形2に分割しよう。
長方形の断面一次モーメントの公式は、\(\frac{bh^{2}}{2}\) なので、それぞれの断面一次モーメントは、次のようになる。
\(G = A \times y_{G}\) なので、\(y_{G} = \frac{G}{A}\)で求められますね。
長方形1の断面一次モーメントを求める
\(G_{x1} =A_{1} \times y_{1}\)なので、
\(G_{x1} =(a \times 3a) \times 1.5a\)
\(G_{x1} = 4.5a^{3}\)
長方形2の断面一次モーメントを求める
\(G_{x2} =A_{2} \times y_{2}\)なので、
\(G_{x2} = (3a \times a) \times (3a + 0.5a)\)
\(G_{x2} = 10.5a^{3}\)
全体の図心を求める
\(G = A \times y_{G}\)で、断面一次モーメントと面積は合計できるので、
\(G_{x1}+S_{x2}) = (A_{1}+A_{2}) \times y_{G}\)にできて、
\(4.5a^{3} + 10.5a^{3}) = (3a^{2} + 3a^{2}) \times y_{G}\)
\(y{G} = 15a^{3} \div 6a^{2}\)
\(y{G} = 2.5a\)
x軸から\(2.5a\)だけ離れた位置が図心ですね。
例題2:三角形と長方形が合わさった図の断面一次モーメント
断面一次モーメントは足し引きできます。
下の図で考えてみましょう。
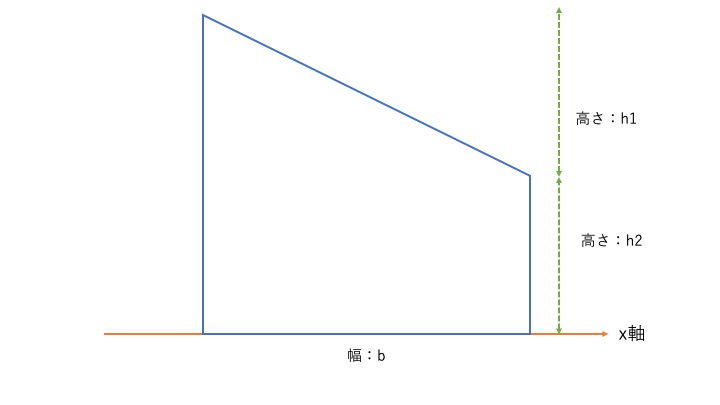
四角形と三角形が組み合わされた図です。わかりやすく分解して書いてみます。
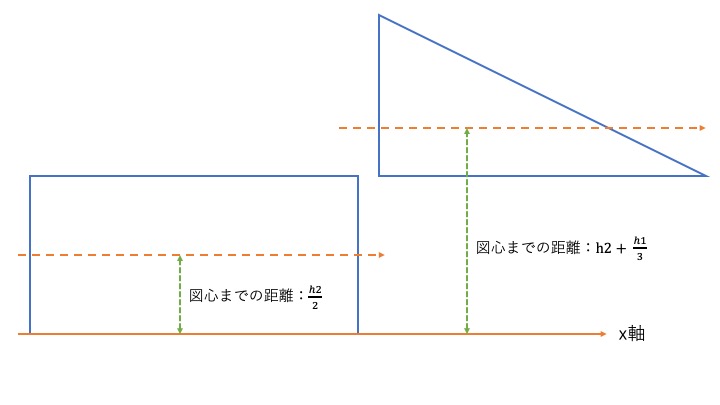
この場合、\( G_{x} = y_{0} \times A \)で計算してみましょう。
図心の位置 \( \times \) 図心までの距離 = 断面1次モーメント
1つずつの断面1次モーメントは以下の通り
これの合計が、全体の図形と同じになるはず。全体の図形の図心を\(y_{0}\)として、
全体の断面1次モーメント = 個々の断面1次モーメントなので、
\( bh_{2}+ \dfrac{bh_{1}}{2} + y_{0} = bh_{2} \frac{h_{2}}{2} + \dfrac{bh_{1}}{2}(h2 + \dfrac{h_{1}}{3}) \)
これを計算すれば全体の図形の図心\(y_{0}\)が求められます。
このようにあらゆる図形で計算できます。
断面二次モーメントとの関係と構造力学での応用

構造力学を学ぶ上で、「断面一次モーメントと断面二次モーメントの違いが分からない」という疑問は非常に多いです。違いを解説します。
断面一次モーメントと断面二次モーメントの違い
| 項目 | 断面一次モーメント (S) | 断面二次モーメント (I) |
| 物理的な意味 | 断面の偏りを示す | 曲げに対する抵抗力を示す |
| 単位 | 長さの3乗 | 長さの4乗 |
| 主な用途 | せん断応力の計算 | 曲げ応力・たわみの計算 |
断面一次モーメントが最も活きる応用:せん断応力
構造物が荷重を受けたとき、部材を「ズレさせよう」とする力がせん断力です。このせん断力に対して部材が耐えられるかをチェックするのがせん断応力の計算であり、断面一次モーメントはここで主役となります。
せん断応力公式: \(tau = \frac{QS}{Ib}\)
\(\tau: せん断応力, Q: せん断力, S: 断面一次モーメント, I: 断面二次モーメント, b: 計算点の幅\)
断面二次モーメントが梁の「曲げの安全性」を示すのに対し、断面一次モーメントは「せん断の安全性」を示すために不可欠な値であると理解してください。
断面一次モーメントについてつまずきやすい疑問を解消するFAQ

最後に、構造力学の学習でよくある、断面一次モーメントに関する疑問をQ&A形式で解消します。
断面一次モーメントと断面係数の関係は?
回答: 断面係数 Z は、「曲げ応力」を計算するための値です。
- \(Z = \frac{I}{y_{max}} (I: 断面二次モーメント, y_{max}: 図心軸から最外縁までの距離)\)
- 断面一次モーメント \(S\) とは、計算に使う目的(せん断 vs 曲げ)が全く異なるため、混同しないようにしましょう。
断面一次モーメントと足し算(重ね合わせ)の原理は成り立つ?
回答: はい、成り立ちます。
- 原理: 複雑な図形は、分割したシンプルな図形の断面一次モーメントを足し合わせる(\sum S_{i}\)ことで求められます(重ね合わせの原理)。
- 重要な例外: ただし、円に穴が開いているドーナツ状の断面などの場合、穴の部分は負(マイナス)の面積として計算し、全体の面積から引く(引き算)ことで求められます。
まとめ:断面1次モーメントをわかりやすく解説

本記事では、断面一次モーメントの定義 \(S=Ay_{G}) から、図心の求め方、T字型やI型断面の分割計算手順までを詳細に解説しました。
構造力学の断面一次モーメントの計算において最も大切な鉄則は「複雑な図形をシンプルな長方形に分割し、基準軸を明確に決めること」です。
【最重要】構造力学の全体像を体系的に学ぶ
「断面一次モーメントは理解できたけれど、構造力学全体の学習計画はどう立てるべきか?」「次にせん断力や曲げモーメントをどう学べばいいか?」という方は、まず挫折しない構造力学の勉強法|テストで点数を取るロードマップをご覧ください。
このロードマップ記事では、支点反力から始まり、断面力、そして応用的な不静定構造物まで、構造力学の知識全体を体系的に解説しています。あなたの学習を最短距離でゴールに導きます。
断面一次モーメントの導出の解説
断面一次モーメンとの詳細な導出過程を解説した記事を用意しました。
構造力学は問題を解いて覚えよう
構造力学のオススメ問題集は『構造力学が苦手な人が読むべきオススメ参考書5選』でまとめていますので、ぜひ参考にしてください。

