力のつり合いがわからないよー
絵で書くとわかりますよ
力のつり合いは絵で書くとわかる
力とは
一般的に『力』とは、物体を動かしたり、壊したりする原因となるものです。
力には２つの要素があります。
- 大きさ
- 向き
この『力』を表すときは、矢印を使います。矢印の向きと長さで力の向きと大きさを表します。
この『力』は合体させたり、分解したりできます。
つり合いとは
力のつり合いとは、動かないことです。
例えば、あなたが椅子に座ったときには、次の２つの力が働きます。
- あなたの体重（重力）
- イスがあなたを支える力
このように、あなたの体重を椅子が支えているから椅子に座ることができます。
つまり、力のつり合いとは、どれだけ力が働いても物体が動いたり、壊れたりしない状況のことを言います。
難しく言えば、力の合力（力が合体した状態）＝ゼロのとき、力はつり合っていると言います。
日常生活も『力』を意識するとつり合いで成り立っていることがわかります。
力のつり合いの解き方
力のつり合いを解くには、次の３つのことが必要です。
- 力を絵で描く
- 力を縦と横に分解する
- 同じ向きの力は合体すると０になる
ひとつずつ見ていきましょう。
力を絵で描く
問題に出てくる図に力を絵で描いてみましょう。
例えば、重力は物体の中心から下向きの矢印を書く、ヒモで物を引っ張るときには引っ張る方向に書くなどです。
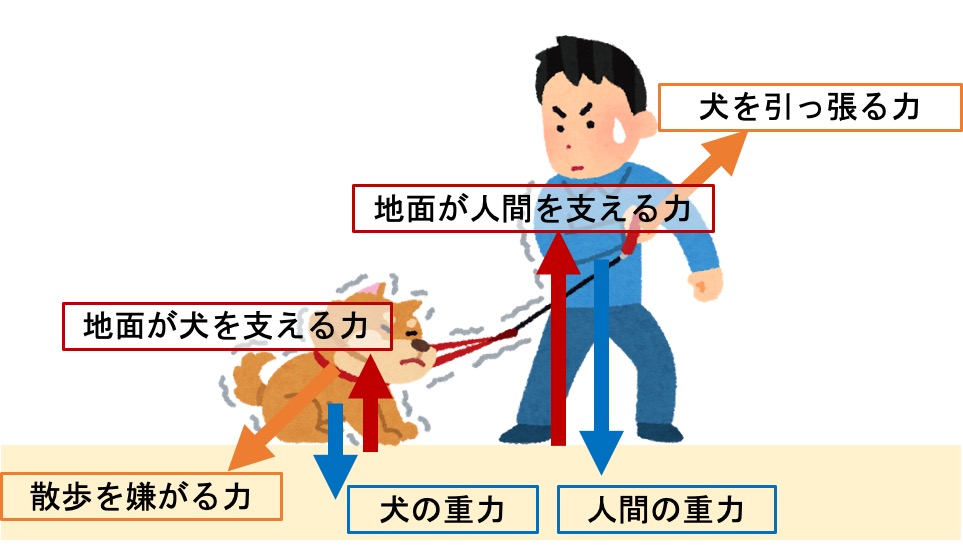
犬が散歩を嫌がっているときは、６個の力がつり合っていると言うことです。
力を縦と横に分解する
力は分解することができます。計算しやすいように、力を縦（鉛直方向）と横（水平方向）に分解します。
上の図では、犬を引っ張る力と散歩を嫌がる力を縦と横に分解できます。
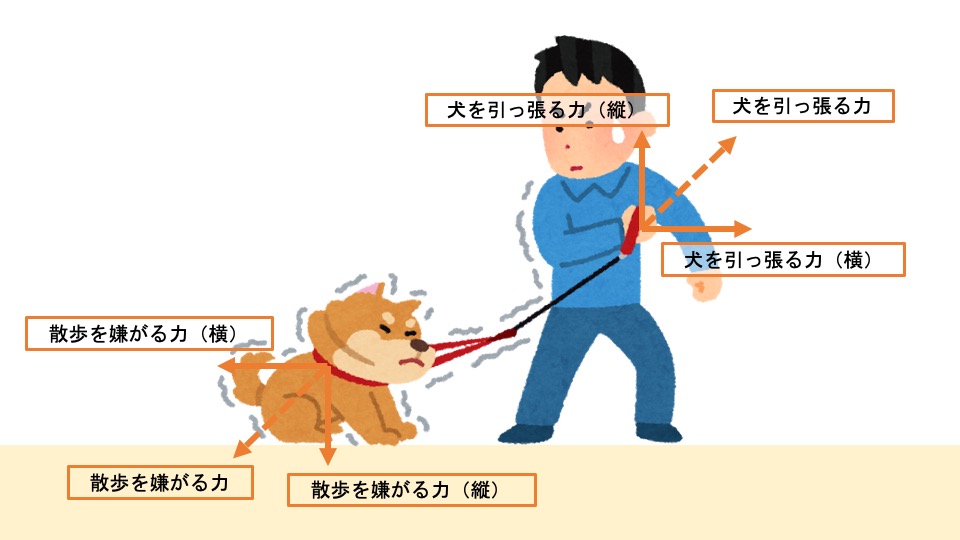
力を縦と横に分解することで、力がたくさんあってもどの向きに働いても簡単に解くことができます。
具体的には、三角関数（sin・cos・tan）を使って分解します。
力の合体が０になる
力を絵で描いて、縦と横に分解しましょう。
それぞれの向きの力の大きさが０になることが力のつり合いの条件です。
散歩を嫌がる犬の例では、縦方向と横方向それぞれの力の合計がゼロになっています。
縦方向の力
- 人間の重力：下向き
- 犬の重力：下向き
- 地面が人間を支える力：上向き
- 地面が犬を支える力：上向き
- 犬を引っ張る力（縦）：上向き
- 散歩を嫌がる力（縦）：下向き
横方向の力
- 犬を引っ張る力（横）：右向き
- 散歩を嫌がる力（横）：左向き
このように、同じ大きさで反対向きの力があるので、散歩を嫌がる犬は動きません。
力のつり合いは絵で描くとわかる【まとめ
力のつり合いを解くためには次の３つが大切です。
- 力を絵で描く
- 力を縦と横に分解する
- 力を合体が０になる
この知識があれば、力のつり合いも怖くありません。
具体的な問題を解きたい方は次の問題集がおすすめです。
- 質の高い問題
- 丁寧で省略のない解説
この問題集はコスパ最強です。
この記事を見ただけでは、力のつり合いは解けるようになりません。
問題を自分の手で解いて、慣れて、わかるようになっていきましょう。